World hardest maths sum
Suggestions or feedback? Images for download on the MIT News office website are made available to non-commercial entities, press and the general public under a Creative Commons Attribution Non-Commercial No Derivatives license.
Well, m aybe. For now, you can take a crack at the hardest math problems known to man, woman, and machine. For more puzzles and brainteasers, check out Puzzmo. In September , news broke regarding progress on this year-old question, thanks to prolific mathematician Terence Tao. Take any natural number, apply f, then apply f again and again. The Conjecture is that this is true for all natural numbers positive integers from 1 through infinity.
World hardest maths sum
In , mathematicians finally solved one of the hardest math problems —one that had stumped them for decades. On the surface, it seems easy. That turned out to be much harder—as in, no one was able to solve for those integers for 65 years until a supercomputer finally came up with the solution to So here are nine more brutally difficult math problems that once seemed impossible, until mathematicians found a breakthrough. In some significant sense, a ball is the simplest of these shapes. It was groundbreaking, yet modest. Perelman rejected both. He said his work was for the benefit of mathematics, not personal gain, and also that Hamilton, who laid the foundations for his proof, was at least as deserving of the prizes. Pierre de Fermat was a 17th-century French lawyer and mathematician. He made claims without proving them, leaving them to be proven by other mathematicians decades, or even centuries, later. These are known as the Pythagorean Triples, like 3,4,5 and 5,12, Fermat famously wrote the Last Theorem by hand in the margin of a textbook, along with the comment that he had a proof, but could not fit it in the margin. For centuries, the math world has been left wondering if Fermat really had a valid proof in mind. For his efforts, Wiles was knighted by Queen Elizabeth II and was awarded a unique honorary plaque in lieu of the Fields Medal, since he was just above the official age cutoff to receive a Fields Medal. Groups can be finite or infinite, and if you want to know what groups of a particular size n look like, it can get very complicated depending on your choice of n.
In some significant sense, a ball is the simplest of these shapes. The usefulness of the Prime Number Theorem is huge. CH has been proven independent, relative to the baseline axioms of math.
Advanced Math Robotics. Schedule a Free Class. Update : This article was last updated on 12th Oct to reflect the accuracy and up-to-date information on the page. The mystical world of mathematics—is home to confounding problems that can make even the most seasoned mathematicians scratch their heads. Problem : Can every map be colored with just four colors so that no two adjacent regions have the same color? Solution Example : The Four Color Theorem was proven with computer assistance, checking numerous configurations to show that four colors are sufficient. Problem : There are no three positive integers a,b,c that satisfies.
For decades, a math puzzle has stumped the smartest mathematicians in the world. When there are two or more unknowns, as is the case here, only the integers are studied. The trick is finding integers that work for all equations, or the numbers for x, y, and z that will all equal k. Over the years, scientists have solved for nearly every integer between 0 and The last two that remained were 33 and Here's a Numberphile video explaining why this problem has proved to be so tricky:. Earlier this year, Andrew Booker of the University of Bristol spent weeks with a supercomputer to finally arrive at a solution for
World hardest maths sum
The Millennium Prize Problems are seven well-known complex mathematical problems selected by the Clay Mathematics Institute in Thus, on the official website of the Clay Mathematics Institute, these seven problems are officially called the Millennium Problems. However, he declined the award as it was not also offered to Richard S. Hamilton , upon whose work Perelman built. The Clay Institute was inspired by a set of twenty-three problems organized by the mathematician David Hilbert in which were highly influential in driving the progress of mathematics in the twentieth century.
Guy with milkshake screaming help
Status : Solved Solution Example: Always switch. This mystery is all about algebraic real numbers. All rational numbers, and roots of rational numbers, are algebraic. Previous item Next item. Some theorems have been proven, which impose a sort of ceiling on the possibilities for large cardinals. Dave Linkletter. Browse By. Problem : Can every even integer greater than 2 be expressed as the sum of two prime numbers? When n hits 4, there are two possibilities. Problem : Can every map be colored with just four colors so that no two adjacent regions have the same color?
Maths is renowned as one of the toughest A-Level subjects. Further Maths is so hard it counts as two A-Levels!
Study finds lands used for grazing can worsen or help climate change Too much livestock on a given amount of land can lead to carbon losses, but appropriate numbers can actually help sequester the carbon. The goal of doing this for polynomials of any degree was noted as early as the 15th century. He said his work was for the benefit of mathematics, not personal gain, and also that Hamilton, who laid the foundations for his proof, was at least as deserving of the prizes. Some theorems have been proven, which impose a sort of ceiling on the possibilities for large cardinals. A packed bunch of spheres will have an average kissing number, which helps mathematically describe the situation. It has other neat closed forms, and appears in hundreds of formulas. Is the Room-Temperature Superconductor Back? Mathematicians have managed to tackle closer and closer versions of the Twin Prime Conjecture. Massachusetts Institute of Technology. Our understanding of prime numbers has flourished in the years since, and Riemann would never have imagined the power of supercomputers. Two mathematicians at the University of Illinois, Urbana-Champaign, Kenneth Appel and Wolfgang Hakan, found a way to reduce the proof to a large, finite number of cases. So if you ever time-travel to ancient Greece, you can tell them their attempts at the angle trisection problem are futile. The History of Pi. He also teaches undergrad classes, and enjoys breaking down popular math topics for wide audiences. There are several hurdles to a full solution, including computational limitations.

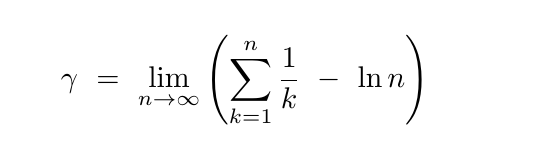
0 thoughts on “World hardest maths sum”