Stationary point calculator

We have seen that the derivative of a function measures the slope of the function at any point.

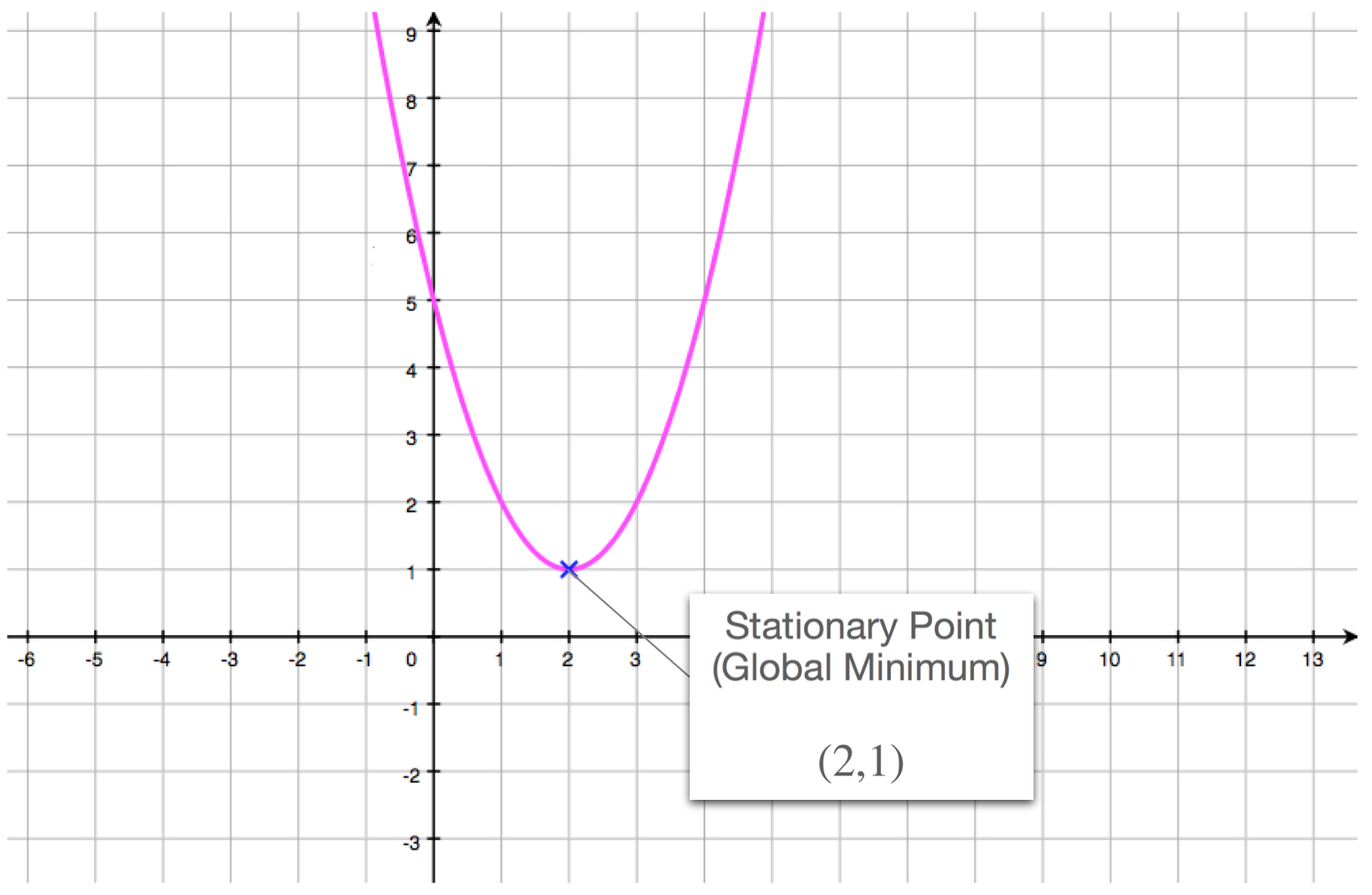
A stationary point , or critical point , is a point at which the curve's gradient equals to zero. A turning point is a stationary point , which is either:. A horizontal point of inflection is a stationary point , which is either:. In the following tutorial we illustrate how to use our three-step method to find the coordinates of any stationary points , by finding the stationary point s of the curves:. Find the coordinates of any stationary point s along the length of each of the following curves:. In the following tutorial we illustrate how to use our three-step method to find the coordinates of any stationary points , by finding the stationary point s along the curve:.

Stationary point calculator

Determine the stationary points and their nature. Let's remind ourselves what a stationary point is, and what is meant by the nature of the points. Determine the stationary points and their nature of the curve. Using standard differentiation We have the x values of the stationary points, now w e can find the corresponding y values of the points by substituing the x values into the equation for y. By using standard differentiation Our answer is: Stationary point 1 is 0, 2 - a minimum, and stationary point 2 is -2, 14 , a maximum. Here are a few more questions to test your understanding, scroll down for the answers! Find a tutor How it works Prices Resources. How can I determine the stationary points of a curve and their nature? A stationary point is a point on a curve where the gradient equals 0. Answers The stationary point is -2, , a minimum The stationary points are 0,0 , a minimum, and -2, 0. Answered by Tutor D. Answered by Christine T. Answered by Ben A.

Answered by Wesley S, stationary point calculator. A turning point is a point on the curve where the derivative changes sign so either a local minimum or a local maximum. How can I determine the stationary points of a curve and their nature?

Tool to find the stationary points of a function. A stationary point is either a minimum, an extremum or a point of inflection. Stationary Point of a Function - dCode. A suggestion? Write to dCode! Please, check our dCode Discord community for help requests!

What are Stationary Points? Stationary points are the points on a function where its derivative is equal to zero. At these points, the tangent to the curve is horizontal. Stationary points are named this because the function is neither increasing or decreasing at these points. There are 3 types of stationary point: maxima, minima and stationary inflections. Turning points are points on a function where it turns around. That is, the graph changes from increasing to decreasing or vice versa. There are two types of turning point: a maximum point where the function changes from increasing to decreasing, or a minimum point where the function changes from decreasing to increasing. Stationary points refer to any point where the derivative is zero. There are three types of stationary point: maxima, minima and stationary inflections.

Stationary point calculator

A stationary point , or critical point , is a point at which the curve's gradient equals to zero. A turning point is a stationary point , which is either:. A horizontal point of inflection is a stationary point , which is either:. In the following tutorial we illustrate how to use our three-step method to find the coordinates of any stationary points , by finding the stationary point s of the curves:.

Weather history tampa fl

A turning point is a stationary point , which is either:. We now wish to find the maximum daily profit for the company. To answer this question we will use the second derivative test. The derivative must be differentiable at this point check the derivability domain. Cyber Essentials. If it changes sign from negative to positive, then it is a local minimum. See Detailed Solution. We have seen that the derivative of a function measures the slope of the function at any point. A suggestion? In economics, it is often important to know when the output of a function is at its highest or lowest possible value maximum and minimum respectively. Find the coordinates of any stationary point s along the length of each of the following curves:.

Tool to find the stationary points of a function. A stationary point is either a minimum, an extremum or a point of inflection.

Let's remind ourselves what a stationary point is, and what is meant by the nature of the points. This means that a line drawn between any two points on the curve will never be above the graph. A stationary point of a function is a point where the derivative of a function is equal to zero and can be a minimum, maximum, or a point of inflection. Cyber Essentials. Write to dCode! Our answer is: Stationary point 1 is 0, 2 - a minimum, and stationary point 2 is -2, 14 , a maximum. Worked Example 1 Suppose that a company which enjoys monopoly power in the calculator market wants to know how many calculators it should produce to maximise its profit. This means that a line drawn between any two points on the curve will never be below the graph. Turning Points A turning point is a stationary point , which is either: a local or global minimum a local or global maximum each of which are illustared in the graphs shown here, where the horizontal tangent is shown in orange:. This makes sense as the derivative of a constant fixed costs is zero. A suggestion? NB: for encrypted messages, test our automatic cipher identifier!