Rhs congruence rule examples

Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure.

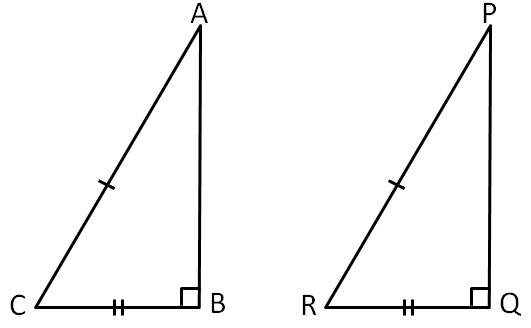
RHS Right angle-Hypotenuse-Side congruence criterion is used to prove the congruence of two right-angled triangles. It states that if the hypotenuse and one side leg of one right triangle are congruent to the hypotenuse and the corresponding side of the other right triangle, then the two right triangles are congruent. Note that this theorem is only applicable to the right-angled triangles. The RHS rule is based on the Pythagoras theorem. In a right triangle, if we know the length of any two sides, we can find the length of the missing side using the Pythagoras theorem, which states that. Thus, if the hypotenuse and one side of one right triangle are congruent to the hypotenuse and corresponding side of another right triangle, the remaining sides will automatically be equal. The RHS Right Angle-Hypotenuse-Side congruence rule states that if the hypotenuse and one side of one right triangle is equal to the hypotenuse and corresponding side of the other right triangle, then the two given right triangles are congruent.

Rhs congruence rule examples

In triangles , you must have studied about congruency of triangles. However, in order to be sure that the two triangles are congruent, we do not necessarily need to have information about all sides and all angles. We use certain rules to prove the congruency of triangles. Look at the triangles given below. Can we place these triangles on each other without any gaps or overlaps? In this mini-lesson, we will explore about RHS congruency criterion by learning about its definition and proof with the help some solved examples and a few interactive questions for you to test your understanding. RHS congruence theorem states that, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle, the two triangles are congruent. This rule is only applicable in right-angled triangles. An important point to note here is that when we keep hypotenuse and any one of the other 2 sides of two right triangles equal, we are automatically getting three similar sides, as all three sides in a right triangle are related to each other and that relation is popularly known as Pythagoras theorem. So, in two right triangles, if the length of base and hypotenuse are 3 units and 5 units respectively, then perpendicular of both the triangles is of length 4 units. If we change the hypotenuse of a triangle, other side-lengths will also be changed to maintain the Pythagoras relation between the sides, i.

What are the Rules of Congruency?

Congruence of triangles is the property of two triangles in which all three corresponding sides and corresponding angles are equal. Two triangles are said to be congruent if and only if they can be overlapped with each other completely. In this article, we are going to learn about the different criteria for the Congruence of Triangles with the help of solved examples. Congruent triangles are triangles that are perfect copies of one another. Various congruence rules are used to prove the congruency in two triangles. Congruent triangles if arranged in proper orientation are mirror images of each other.

As an avid student of geometry, you likely understand the importance of congruence in shapes and figures. One of the most fundamental rules for determining congruence is the rhs congruence rule. Mastering this rule will open a deeper understanding of triangle congruence and similarity, providing a foundation for more complex geometric proofs and problem solving. In this article, you will explore the rhs congruence rule in detail. Beginning with the definition and formula, you will then see step-by-step how to apply the rule through examples and practice problems. With consistent application of the rhs congruence rule, you will strengthen your geometric reasoning and build confidence in your ability to determine congruence between triangles. Read on to discover how this essential rule of geometry will expand your mathematical skills.

Rhs congruence rule examples

RHS Right angle-Hypotenuse-Side congruence criterion is used to prove the congruence of two right-angled triangles. It states that if the hypotenuse and one side leg of one right triangle are congruent to the hypotenuse and the corresponding side of the other right triangle, then the two right triangles are congruent. Note that this theorem is only applicable to the right-angled triangles. The RHS rule is based on the Pythagoras theorem. In a right triangle, if we know the length of any two sides, we can find the length of the missing side using the Pythagoras theorem, which states that. Thus, if the hypotenuse and one side of one right triangle are congruent to the hypotenuse and corresponding side of another right triangle, the remaining sides will automatically be equal. The RHS Right Angle-Hypotenuse-Side congruence rule states that if the hypotenuse and one side of one right triangle is equal to the hypotenuse and corresponding side of the other right triangle, then the two given right triangles are congruent. By understanding this rule, we can determine the congruence of two right triangles based on the congruence of their hypotenuse and one corresponding leg. Thus, we cannot say that the two triangles are congruent by RHS congruence rule. The information is not sufficient.

Creepy places on google maps coordinates

But hurry up, because the offer is ending on 29th Feb! The RHS Right Angle-Hypotenuse-Side congruence rule states that if the hypotenuse and one side of one right triangle is equal to the hypotenuse and corresponding side of the other right triangle, then the two given right triangles are congruent. What is SSS congruency of triangles? Save Article. Please Login to comment Show that BD bisects AC at right angles. Omg September 23, at am. Our Journey. Relations And Functions. United Kingdom. RHS congruence theorem states that, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle, the two triangles are congruent.

It states the criteria for any two right-angle triangles to be congruent. This rule states that if in two right triangles, the hypotenuse and one side of one triangle are equal to the hypotenuse and one corresponding side of the other triangle, then the triangles are congruent. In this article, we will discuss the criteria of congruence of right-angle triangles in detail including proof and examples.

AAS Angle-Angle-Side congruence states that if two angles and a non-included side of one triangle are equal to the corresponding two angles and side of another triangle, then the two triangles are congruent. In RHS congruency, if only two sides i. Did not receive OTP? Congruency of triangles means that: All corresponding angles are equal. Also, learn about Congruent Figures here. Hence, the congruence of triangles can be evaluated by knowing only three values out of six. Download Now. Prove that it lies on the bisector of that angle. Correct Incorrect. Like Article Like.