Positive real numbers
Real numbers are simply the combination of rational and irrational numbers, positive real numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. At the same time, the imaginary numbers positive real numbers the un-real numbers, which cannot be expressed in the number line and are commonly used to represent a complex number. Some of the examples of real numbers are 23,6.
In mathematics , a real number is a number that can be used to measure a continuous one- dimensional quantity such as a distance , duration or temperature. Here, continuous means that pairs of values can have arbitrarily small differences. The real numbers are fundamental in calculus and more generally in all mathematics , in particular by their role in the classical definitions of limits , continuity and derivatives. The rest of the real numbers are called irrational numbers. Real numbers can be thought of as all points on a line called the number line or real line , where the points corresponding to integers Conversely, analytic geometry is the association of points on lines especially axis lines to real numbers such that geometric displacements are proportional to differences between corresponding numbers.
Positive real numbers
Wiki User. Natural numbers extend from 1 to positive infinity. Real numbers are all numbers between negative infinity and positive infinity. When two negative real numbers are multiplied together, the product is a positive real number. Real numbers include positive and negative numbers, integers and fractions, rational and irrational numbers. Real numbers include fractional and decimal numbers. So the closest-to-zero positive real number would be 0. The most common definition of 'natural' numbers is: The counting numbers. According to that definition, all natural numbers are positive. Real numbers are all positive numbers except zero.
In real numbers Class 9, the common concepts introduced include representing real numbers on a number line, operations on real numbers, positive real numbers, properties of real numbers, and the law of exponents for real numbers. Continue Learning about Other Math.
This ray is used as reference in the polar form of a complex number. It inherits a topology from the real line and, thus, has the structure of a multiplicative topological group or of an additive topological semigroup. In the study of physical magnitudes, the order of decades provides positive and negative ordinals referring to an ordinal scale implicit in the ratio scale. Among the levels of measurement the ratio scale provides the finest detail. The division function takes a value of one when numerator and denominator are equal.
Real number is any number that can be found in the real world. We find numbers everywhere around us. Natural numbers are used for counting objects, rational numbers are used for representing fractions, irrational numbers are used for calculating the square root of a number, integers for measuring temperature, and so on. These different types of numbers make a collection of real numbers. In this lesson, let us learn all about what are real numbers, the subsets of real numbers along with real numbers examples. Any number that we can think of, except complex numbers, is a real number. For example, 3, 0, 1. Real numbers include rational numbers like positive and negative integers, fractions, and irrational numbers. Now, which numbers are not real numbers? These numbers include the set of complex numbers , C.
Positive real numbers
Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. At the same time, the imaginary numbers are the un-real numbers, which cannot be expressed in the number line and are commonly used to represent a complex number. Some of the examples of real numbers are 23, , 6. In this article, we are going to discuss the definition of real numbers, the properties of real numbers and the examples of real numbers with complete explanations.
Hair undercut man bun
The set of definable numbers is broader, but still only countable. Again, the existence of such a well-ordering is purely theoretical, as it has not been explicitly described. The definition of real numbers itself states that it is a combination of both rational and irrational numbers. In the table given below, all the real numbers formulas i. The real numbers form an ordered field. A real number is called computable if there exists an algorithm that yields its digits. Conversely, analytic geometry is the association of points on lines especially axis lines to real numbers such that geometric displacements are proportional to differences between corresponding numbers. Article Talk. Resources Leaderboard All Tags Unanswered. All Rights Reserved.
This ray is used as reference in the polar form of a complex number. It inherits a topology from the real line and, thus, has the structure of a multiplicative topological group or of an additive topological semigroup. In the study of physical magnitudes, the order of decades provides positive and negative ordinals referring to an ordinal scale implicit in the ratio scale.
Three other order relations are also commonly used:. Tools Tools. The set of rational numbers is not complete. Such a decimal representation specifies a unique nonnegative real number as the least upper bound of the decimal fractions that are obtained by truncating the sequence. FREE Signup. The supremum axiom of the reals refers to subsets of the reals and is therefore a second-order logical statement. The study refers to hyperbolic coordinates in Q. Retrieved The subsets of real numbers include rational numbers, irrational numbers, natural numbers, and whole numbers. Share Share Share Call Us. Classification List.

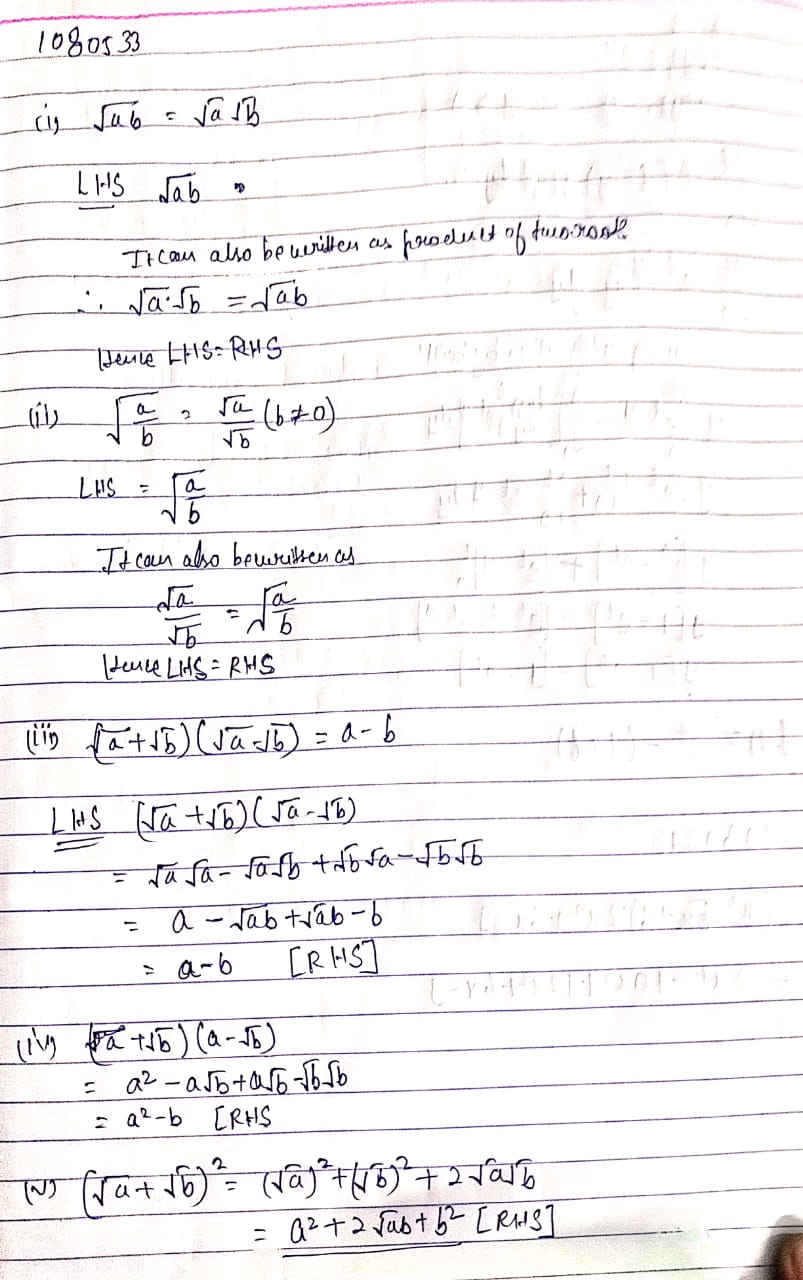
Curiously, and the analogue is?
You are not right. I can defend the position. Write to me in PM.