Laplace transform of unit step function
Online Calculus Solver ».
Online Calculus Solver ». IntMath f orum ». In engineering applications, we frequently encounter functions whose values change abruptly at specified values of time t. One common example is when a voltage is switched on or off in an electrical circuit at a specified value of time t. The switching process can be described mathematically by the function called the Unit Step Function otherwise known as the Heaviside function after Oliver Heaviside. That is, u is a function of time t , and u has value zero when time is negative before we flip the switch ; and value one when time is positive from when we flip the switch.
Laplace transform of unit step function
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Properties of the Laplace transform. About About this video Transcript. Introduction to the unit step function and its Laplace Transform. Created by Sal Khan. Want to join the conversation? Log in. Sort by: Top Voted. Posted 11 years ago. I keep getting stuck around 20 min where Sal explains that x is just a letter. Thank you for any help :. Downvote Button navigates to signup page.
I hope this helps someone. I should have some standards. It is the function f that is varying.
To productively use the Laplace Transform, we need to be able to transform functions from the time domain to the Laplace domain. We can do this by applying the definition of the Laplace Transform. Our goal is to avoid having to evaluate the integral by finding the Laplace Transform of many useful functions and compiling them in a table. Thereafter the Laplace Transform of functions can almost always be looked by using the tables without any need to integrate. A table of Laplace Transform of functions is available here.
Online Calculus Solver ». IntMath f orum ». We saw some of the following properties in the Table of Laplace Transforms. We write the function using the rectangular pulse formula. We also use the linearity property since there are 2 items in our function. This is an exponential function see Graphs of Exponential Functions. From trigonometry , we have:. Disclaimer: IntMath.
Laplace transform of unit step function
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Properties of the Laplace transform. About About this video Transcript.
Homebase wallpaper
Now, what were we doing here the whole time? Took me a while to understand this but I finally figured it out. And dt is the same thing is dx. So how can we construct this yellow function, where it's essentially a shifted version of this green function, but it's zero below c? And I'll show you how this is a very useful result to take a lot of Laplace transforms and to invert a lot of Laplace transforms. So f of 0, it should be the same. To productively use the Laplace Transform, we need to be able to transform functions from the time domain to the Laplace domain. So you get x plus c there, and then times the function f of t minus c, but we said t minus c is the same thing as x. Later, on this page So let me rewrite the result that we proved just now. Let me write that. I hope this helps someone. This creates math problem solver thats more accurate than ChatGPT, more flexible than a calculator, and faster answers than a human tutor. How is the unit step function an actual function?
To productively use the Laplace Transform, we need to be able to transform functions from the time domain to the Laplace domain.
So f of 0, it should be the same. Well, let's say we wanted to figure out the Laplace transform of the unit step function that starts up at pi of t. Such a function may be described using the shifted aka delayed unit step function. Problem Solver provided by Mathway. We want it to jump up again. So essentially what we have here is a combination of zero all the way, and then we have a shifted f of t. Yes, Heaviside function Now, what if I wanted to do something a little bit fancier? This is the Laplace transform of f of t times some scaling factor, and that's what we set out to show. Posted 4 years ago. So if we want to essentially find the area under this curve, we can ignore all the stuff that happens before c. Rather that for use with the Laplace transform, we are only interested in c values greater than zero since, as you mentioned, the transform is only concerned with t [0,inf. Then if you multiply both sides by dt, you get dx is equal to dt, and that's a nice substitution. What's the Laplace transform of-- well, I could write it as f of t or f of x.

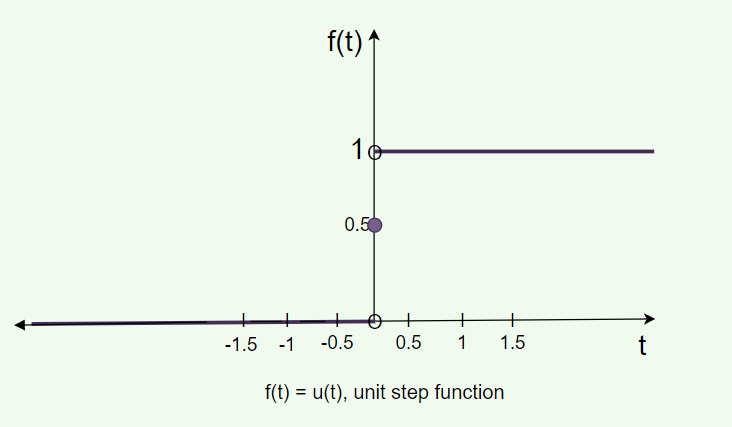
Also that we would do without your brilliant idea