Khan academy finite element method

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. About About this video Transcript. Proving an expression for the sum of all positive integers up to and including n by induction.

Khan academy finite element method

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Modeling situations with differential equations. About About this video Transcript. Differential equations are equations that relate a function with one or more of its derivatives. This means their solution is a function! Learn more in this video. Want to join the conversation? Log in. Sort by: Top Voted.

The body, i.

Personalise your OpenLearn profile, save your favourite content and get recognition for your learning. Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available. The basic principles underlying the FEM are relatively simple. Consider a body or engineering component through which the distribution of a field variable, e.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Equivalent systems of equations and the elimination method. About About this video Transcript. An old video where Sal introduces the elimination method for systems of linear equations.

Khan academy finite element method

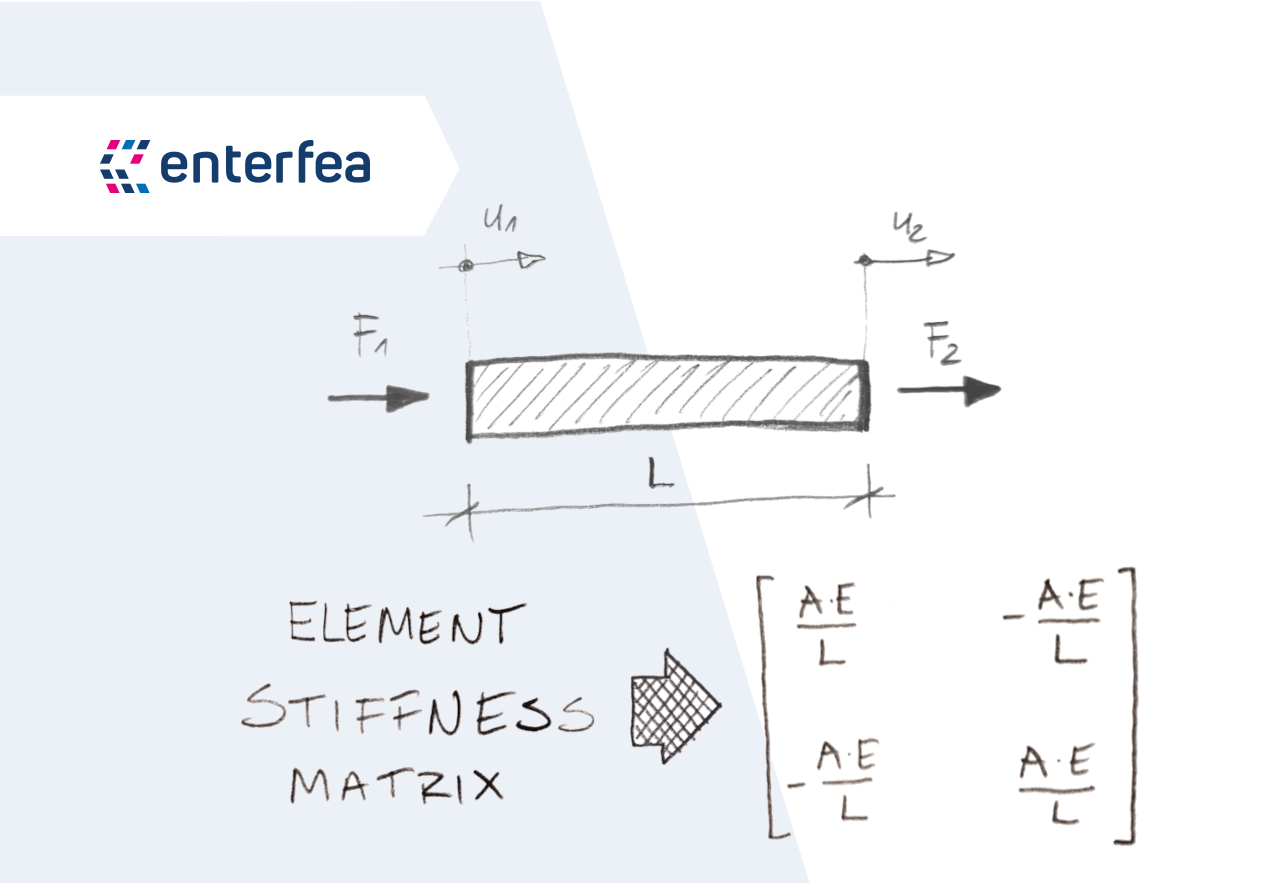
The finite element method FEM is a powerful technique originally developed for numerical solution of complex problems in structural mechanics , and it remains the method of choice for complex systems. In the FEM, the structural system is modeled by a set of appropriate finite elements interconnected at discrete points called nodes. Elements may have physical properties such as thickness, coefficient of thermal expansion , density , Young's modulus , shear modulus and Poisson's ratio. The origin of finite method can be traced to the matrix analysis of structures [1] [2] where the concept of a displacement or stiffness matrix approach was introduced. Finite element concepts were developed based on engineering methods in s. The finite element method obtained its real impetus in the s and s by John Argyris , and co-workers; at the University of Stuttgart , by Ray W. Straight or curved one-dimensional elements with physical properties such as axial, bending, and torsional stiffnesses. This type of element is suitable for modeling cables, braces, trusses, beams, stiffeners, grids and frames. Straight elements usually have two nodes, one at each end, while curved elements will need at least three nodes including the end-nodes. The elements are positioned at the centroidal axis of the actual members.

October 30 zodiac sign

Ergo Proxy. This figure shows a side-on view of a rectangular plate with a hole in it. Posted 7 years ago. And I encourage you to pause this video right now and find the first derivative of y one, and the second derivative of y one, and verify that it does indeed satisfy this differential equation. Close There is currently an issue with creating new accounts. The body, i. Forever Learner. We are assuming that we already have a formula for this. It is done in two steps. Flag Button navigates to signup page. Why is that? But in this case, we are saying this is true for all positive integers. I noticed the function abruptly stopped at the y-axis and did not extend into the second or third quatrains at all.

Forgot password? New user?

Video transcript I'm going to define a function S of n and I'm going to define it as the sum of all positive integers including N. We'll verify that these indeed are solutions for I guess this is really just one differential equation represented in different ways. Unit 3: Alternate coordinate systems bases. The elements are assumed to be connected to one another, but only at interconnected joints, known as nodes. Modeling situations with differential equations. I recognized that some values are complex and cannot be graphed, yet some can, such as -1, -1 or -2, 0. Actually let me move this over a little bit. Now at this step right over here you can factor out a k plus 1. Induction always took a little while for me to fully get used to. In the next few videos, we'll explore this more. We are assuming that this is going to simplify to k times k plus 1 over 2. So we showed , we proved our base case. And it's going to be all of this over 2.