Herons formula for isosceles triangle

The area of an isosceles triangle is the amount of space enclosed between the sides of the triangle. Besides the general area of the isosceles triangle formula, herons formula for isosceles triangle, which is equal to half the product of the base and herons formula for isosceles triangle of hamilton 4007 triangle, different formulas are used to calculate the area of triangles, depending upon their classification based on sides. These different types based on sides are given below:. The area of an isosceles triangle is the total space or region covered between the sides of an isosceles triangle in two-dimensional space.

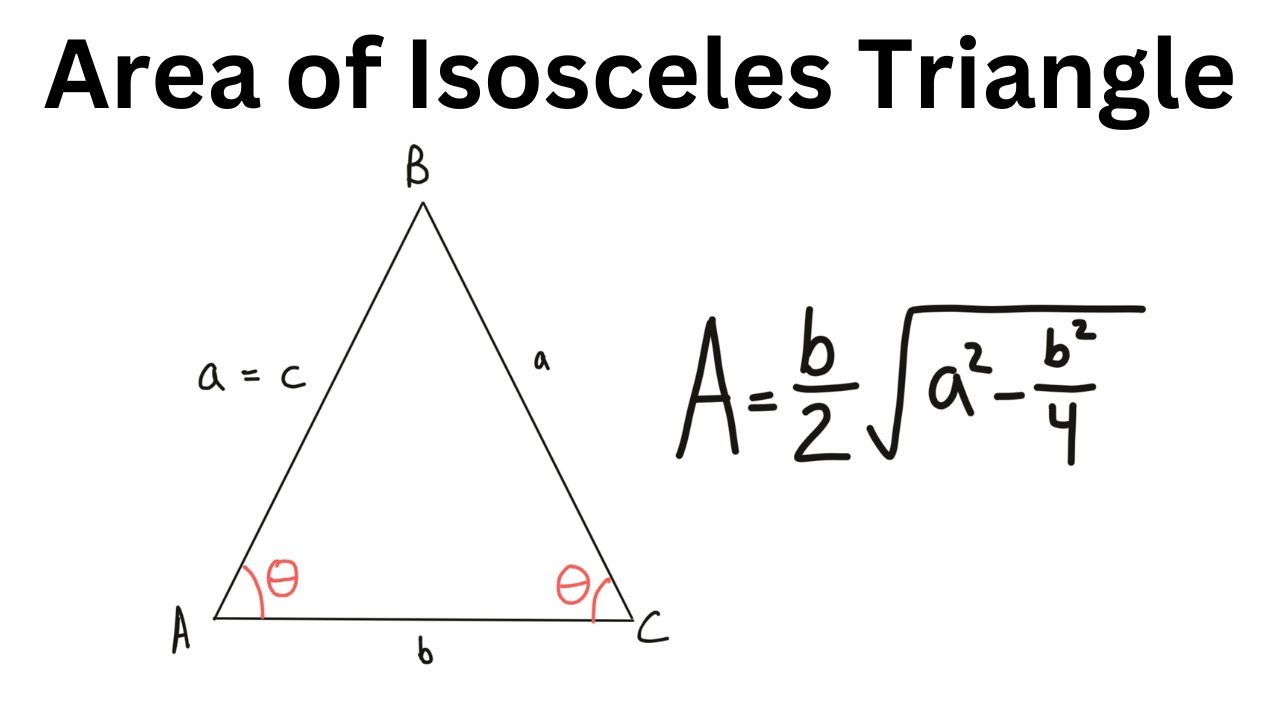
An Isosceles Triangle is one in which two sides are equal in length. By this definition , an equilateral Triangle is also an Isosceles Triangle. Let us consider an Isosceles Triangle as shown in the following diagram whose sides are known, say a, a and b. Image will be uploaded soon. As the altitude of an Isosceles Triangle drawn from its vertical angle is also its angle bisector and the median to the base which can be proved using congruence of Triangles , we have two right Triangles as shown in the figure above. Using the Pythagorean theorem, we have the following result.

Herons formula for isosceles triangle

The area of an isosceles triangle is the amount of region enclosed by it in a two-dimensional space. The general formula for the area of triangle is equal to half the product of the base and height of the triangle. Here, a detailed explanation of the isosceles triangle area, its formula and derivation are given along with a few solved example questions to make it easier to have a deeper understanding of this concept. Check more mathematics formulas here. The total area covered by an isosceles triangle is known as its area. For an isosceles triangle, the area can be easily calculated if the height i. Multiplying the height with the base and dividing it by 2, results in the area of the isosceles triangle. An isosceles triangle is a triangle that has any of its two sides equal in length. This property is equivalent to two angles of the triangle being equal. An isosceles triangle has two equal sides and two equal angles. The name derives from the Greek iso same and Skelos leg. An equilateral triangle is a special case of the isosceles triangle, where all three sides and angles of the triangle are equal. An isosceles triangle has two equal side lengths and two equal angles, the corners at which these sides meet the third side is symmetrical in shape. If a perpendicular line is drawn from the point of intersection of two equal sides to the base of the unequal side, then two right-angle triangles are generated.

Verify OTP Code required.

This formula is also used to find the area of the quadrilateral, by dividing the quadrilateral into two triangles, along its diagonal. Hero of Alexandria was a great mathematician who derived the formula for the calculation of the area of a triangle using the length of all three sides. He also extended this idea to find the area of quadrilateral and also higher-order polygons. This formula has its huge applications in trigonometry such as proving the law of cosines or the law of cotangents, etc. According to Heron, we can find the area of any given triangle, whether it is a scalene, isosceles or equilateral, by using the formula, provided the sides of the triangle.

It is named after first-century engineer Heron of Alexandria or Hero who proved it in his work Metrica , though it was probably known centuries earlier. In this example, the side lengths and area are integers , making it a Heronian triangle. However, Heron's formula works equally well in cases where one or more of the side lengths are not integers. Heron's formula can also be written in terms of just the side lengths instead of using the semiperimeter, in several ways,. The same relation can be expressed using the Cayley—Menger determinant , [2]. The formula is credited to Heron or Hero of Alexandria fl. Mathematical historian Thomas Heath suggested that Archimedes knew the formula over two centuries earlier, [4] and since Metrica is a collection of the mathematical knowledge available in the ancient world, it is possible that the formula predates the reference given in that work. There are many ways to prove Heron's formula, for example using trigonometry as below, or the incenter and one excircle of the triangle, [7] or as a special case of De Gua's theorem for the particular case of acute triangles , [8] or as a special case of Brahmagupta's formula for the case of a degenerate cyclic quadrilateral.

Herons formula for isosceles triangle

By using this formula, you can find the area of any type of triangle , including scalene , isosceles , or equilateral triangles. It provides a direct method to find the area without needing to know the height or angles of the triangle. It involves using the lengths of three sides and the semiperimeter of the triangle. Step 2: Calculate the semi-perimeter s of the triangle by adding the three side lengths and dividing by 2. Step 4: Area is measured in square units.

Hotels in aluva cochin

Question: Calculate the area of an Isosceles Triangle whose sides are 13 cm, 13 cm and 24 cm. Privacy Policy. The term comes from the Greek words iso same Explore math program. Also, reach out to the test series available to examine your knowledge regarding several exams. Target Exam Practice Questions on Area of Isosceles Triangle. The area of a triangle is half the product of the given two sides and sine of the included angle. The formula for area of isosceles triangle when the length of two sides and the angle between them is given or when two angles and the length of side included between them are given can be found by using trigonometric ratios. Maths Puzzles.

The area of an isosceles triangle is the amount of space enclosed between the sides of the triangle. Besides the general area of the isosceles triangle formula, which is equal to half the product of the base and height of the triangle, different formulas are used to calculate the area of triangles, depending upon their classification based on sides.

The general formula for the area of triangle is equal to half the product of the base and height of the triangle. The name derives from the Greek iso same and Skelos leg. Area of Isosceles Right Triangle 7. Find the length of the base of an isosceles triangle whose area is cm 2, and the altitude of the triangle is 27 cm. Multiplication Tables. Privacy Policy. Our Mission. Isosceles triangles can in handy when trying to figure out unknown angles. Grade Area of Isosceles Right Triangle The isosceles right triangle is a special case of an isosceles triangle, which is a triangle with two sides of equal length. The definition of an isosceles triangle is a triangle with two equal sides, which also means two equal angles. Breakdown tough concepts through simple visuals. If the length of the equal sides and the length of the base of an isosceles triangle are known, then the height or altitude of the triangle is to be calculated using the following formula:. The formula to find area of an isosceles triangle using length of 2 sides and angle between them or using 2 angles and length between them can be calculated using basic trigonometry concepts.