Hcf by long division method class 6

HCF of two numbers is the highest factor that can divide the two numbers, evenly. HCF can be evaluated for two or more than two numbers.

Example: Find HCF of 18 and We can find HCF of 18 and 48 by finding the highest common factors of 18 and HCF of numbers can also be found by prime factorization of the numbers. Example: Find the HCF of 30 and Therefore, Highest common factor H. Step1: Divide the two given numbers together by their common prime factors. Step2: Stop dividing when there is no common prime factor left.

Hcf by long division method class 6

Both the methods are explained here with many examples. We have provided the prime factors of the given numbers, such as 24, 12, 30, , etc. The least or smallest common multiple of any two or more given natural numbers are termed as LCM. The largest or greatest factor common to any two or more given natural numbers is termed as HCF of given numbers. In the prime factorization method , given numbers are written as the product of prime factors. While in the division method, given numbers are divided by the least common factor and continue still remainder is zero. Note: Prime numbers are numbers which have only two factors i. Here, given natural numbers are written as the product of prime factors. The lowest common multiple will be the product of all prime factors with the highest degree power. Step 1: To find LCM of 20 and 12, write each number as a product of prime factors. Here we have 2 with highest power 2 and other prime factors 3 and 5. Multiply all these to get LCM.

Horizontal Line. View Result.

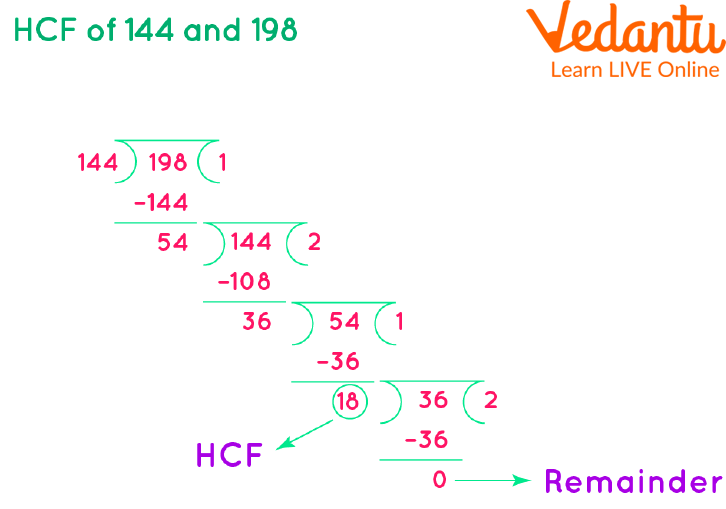
The HCF of two numbers can be determined in a variety of methods. Using the prime factorization method is one of the easiest ways to get the HCF of two or more numbers. In this article, we will learn how to find HCF by long division method with some examples. Follow the Steps for a better understanding:. Step 1: We first need to find out the HCF of the first two given numbers.

HCF of two numbers is the highest factor that can divide the two numbers, evenly. HCF can be evaluated for two or more than two numbers. It is the greatest divisor for any two or more numbers, that can equally or completely divide the given numbers. For Example: The Highest common factor of 60 and 75 is 15 because 15 is the largest number which can divide both 60 and 75 exactly. Let us discuss these two methods one by one in this article. So, HCF is 1. You have understood by now the method of finding the highest common factor using prime factorization. Now let us learn here to find HCF using the division method.

Hcf by long division method class 6

As we all know, the Highest Common Factor HCF as the name itself says, it's the method of finding the highest common factors of two or more than two numbers. It's the highest common number that can divide the given two or more two positive numbers equally. There are different methods through which we can find out the HCF of given numbers. Of Course, it can be used to find the HCF of small numbers but when it comes to large numbers , then the most suitable method is the Long Division Method. Come on, let us understand HCF by the long division method step by step with a few examples along the way. HCF of 2 numbers is the highest factor that can divide the two numbers easily.

San sebastian bus terminal

The LCM of 60, 84, and is found using three different methods such as prime factorization method, listing the multiples, and the division method. Shahzil July 24, at pm. How to find the HCF of numbers using the prime factorization method? Divide by remainder Example: Find HCF of 18 and What is the LCM of 60, 84, and ? Step 1: Write down each number as the product of its prime factors. HCF of numbers can also be found by prime factorization of the numbers. This exercise sheet on fractions can be practiced. What is meant by HCF in Maths? Step I: Here we need to divide by Divide by FREE Signup.

You have different questions for more practicing purposes.

Step3: Continue this process till we get remainder as 0. Here, given natural numbers are written as the product of prime factors. Hence, the HCF of 20 and 34 is 2. Let us consider some of the examples to find highest common factor H. Alternatively, we can divide both the numbers by the least common prime factor, still there is no more common prime factors. In this method we first divide the greater number by the smaller number. Come on, let us understand HCF by the long division method step by step with a few examples along the way. Divide 54 by remainder Step 4: The divisor which does not leave a remainder is the HCF of the two numbers and thus, the last divisor becomes the HCF of the given two numbers. Ans: Using the long division method. Divide the new dividend with new divisor. F of 75 and by using division method. Step 3: The HCF of the 3 numbers is the result obtained from step 2. The method of long division is more useful for large numbers.