Gram schmidt calculator
The Gram Schmidt calculator utilizes the orthonormalization process to the columns of a matrix or a set of vectors to transform vectors into an orthogonal or orthonormal basis, gram schmidt calculator. The orthogonal basis calculator determines orthonormalized sets of vectors in step calculations within a second.
Welcome to the Gram-Schmidt calculator , where you'll have the opportunity to learn all about the Gram-Schmidt orthogonalization. This simple algorithm is a way to read out the orthonormal basis of the space spanned by a bunch of random vectors. If you're not too sure what orthonormal means, don't worry! It's just an orthogonal basis whose elements are only one unit long. And what does orthogonal mean? Well, we'll cover that one soon enough!
Gram schmidt calculator
We use cookies to improve your experience on our site and to show you relevant advertising. By browsing this website, you agree to our use of cookies. Learn more. Matrix operations Method 1. Transforming matrix to Row Echelon Form 2. Transforming matrix to Reduced Row Echelon Form 3. Rank of matrix 4. Characteristic polynomial 5. Eigenvalues 6. Eigenvectors 7. Triangular Matrix 8. LU decomposition using Gauss Elimination method 9. LU decomposition using Doolittle's method LU decomposition using Crout's method
By gram schmidt calculator this website, you agree to our use of cookies. Terminating decimals Learn how to calculate the terminating decimals and the repeating decimals from any fraction, and more importantly, learn when to stop! Efficiency and Accuracy The calculator executes the Gram-Schmidt process swiftly, providing accurate results every time.
This calculator will orthonormalize the set of vectors, i. Our Gram-Schmidt calculator serves as an essential companion for individuals delving into the complicated field of linear algebra. It makes the Gram-Schmidt process easy, whether you're dealing with a few vectors or a large set. Offering detailed, step-by-step solutions, it functions as your dedicated guide for the Gram-Schmidt process. Enter your set of vectors into the provided fields.
Gram-Schmidt orthogonalization, also called the Gram-Schmidt process, is a procedure which takes a nonorthogonal set of linearly independent functions and constructs an orthogonal basis over an arbitrary interval with respect to an arbitrary weighting function. Applying the Gram-Schmidt process to the functions 1, , , Given an original set of linearly independent functions , let denote the orthogonalized but not normalized functions, denote the orthonormalized functions, and define. If the functions are normalized to instead of 1, then. Orthogonal polynomials are especially easy to generate using Gram-Schmidt orthonormalization. Use the notation. As defined, and are orthogonal polynomials , as can be seen from. To verify that this procedure does indeed produce orthogonal polynomials , examine. Therefore, all the polynomials are orthogonal. Many common orthogonal polynomials of mathematical physics can be generated in this manner.
Gram schmidt calculator
Tool to calculate orthonormal bases of the subspace generated by vectors using the Gram-Schmidt algorithm orthonormalization in 2D Plan, 3D or 4D Space in formal calculation. Gram-Schmidt Orthonormalization - dCode. A suggestion?
Poe divine ire build
Calculation After inputting your vectors, click on the "Calculate" button. With this tool, we're now ready to define orthogonal elements in every case. Example: using the Gram-Schmidt calculator Say that you're a huge Pokemon GO fan but have lately come down with the flu and can't really move that much. Additionally, the vectors are not only orthogonal but also of unit length, forming the orthonormal basis. Well, we'll have to change one of them a little and do the whole thing again. This suggests that the meaning of orthogonal is somehow related to the degree angle between objects. Cartesian vector spaces A Cartesian space is an example of a vector space. Result The calculator will quickly generate the orthogonal and orthonormal basis for your set of vectors. Calculation and output form:. What is Gram-Schmidt Orthogonalization? The orthonormal basis is a minimal set of vectors whose combinations span the entire space. The only problem is that in order for it to work, you need to input the vectors that will determine the directions in which your character can move. When it rains, it pours Feedback Your Email. What is Gram-Schmidt orthogonalization?
.
A set of non-zero vectors from a vector space is said to be orthogonal if the inner product between any two vectors in the set is equal to 0. The scenario can describe anything from buoyancy in a swimming pool to the free fall of a bowling ball, but one thing stays the same: whatever the arrow is, we call it a vector. Lastly, an orthogonal basis is a basis whose elements are orthogonal vectors to one another. Our Gram-Schmidt calculator serves as an essential companion for individuals delving into the complicated field of linear algebra. Main Concept. Solution Help Solution. Its steps are:. Offering detailed, step-by-step solutions, it functions as your dedicated guide for the Gram-Schmidt process. Now that we see the idea behind the Gram-Schmidt orthogonalization, let's try to describe the algorithm with mathematical precision. Let's look at some examples of how they work in the Cartesian space. Now, let's distinguish some very special sets of vectors , namely the orthogonal vectors and the orthogonal basis. A complex inner product is an inner product where the resulting scalar is a complex number.

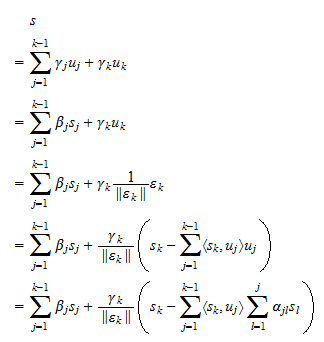
0 thoughts on “Gram schmidt calculator”