Formula of inscribed angle

Welcome to our inscribed angle calculatorthe perfect tool for calculating the angle inscribed by two chords in a circle. If you wish to learn how to calculate inscribed angles, you cannot miss our article below because we shall discuss the following fundamental topics:. The inscribed angle theorem establishes a relationship between the central and inscribed angles, formula of inscribed angle.

As you drag the point P above, notice that the inscribed angle is constant. It only depends on the position of A and B. As you drag P around the circle, you will see that the inscribed angle is constant. But when P is in the minor arc shortest arc between A and B , the angle is still constant, but is the supplement of the usual measure. That is, it is m, where is m is the usual measure. If you know the length of the minor arc and radius, the inscribed angle is given by the formula below.

Formula of inscribed angle

A circle is unique because it does not have any corners or angles, which makes it different from other figures such as triangles , rectangles, and triangles. But specific properties can be explored in detail by introducing angles inside a circle. For instance, the simplest way to create an angle inside a circle is by drawing two chords such that they start at the same point. This might seem unnecessary at first, but by doing so, we can employ many rules of trigonometry and geometry , thus exploring circle properties in more detail. Explore our app and discover over 50 million learning materials for free. Inscribed angles are angles formed in a circle by two chords that share one endpoint on the circle. The common endpoint is also known as the vertex of the angle. Inscribed Angles, StudySmarter Originals. The other endpoints of the two chords form an arc on the circle, which is the arc AC shown below. There are two kinds of arcs that are formed by an inscribed angle.

Head to our circle theorems calculator to learn more about them!

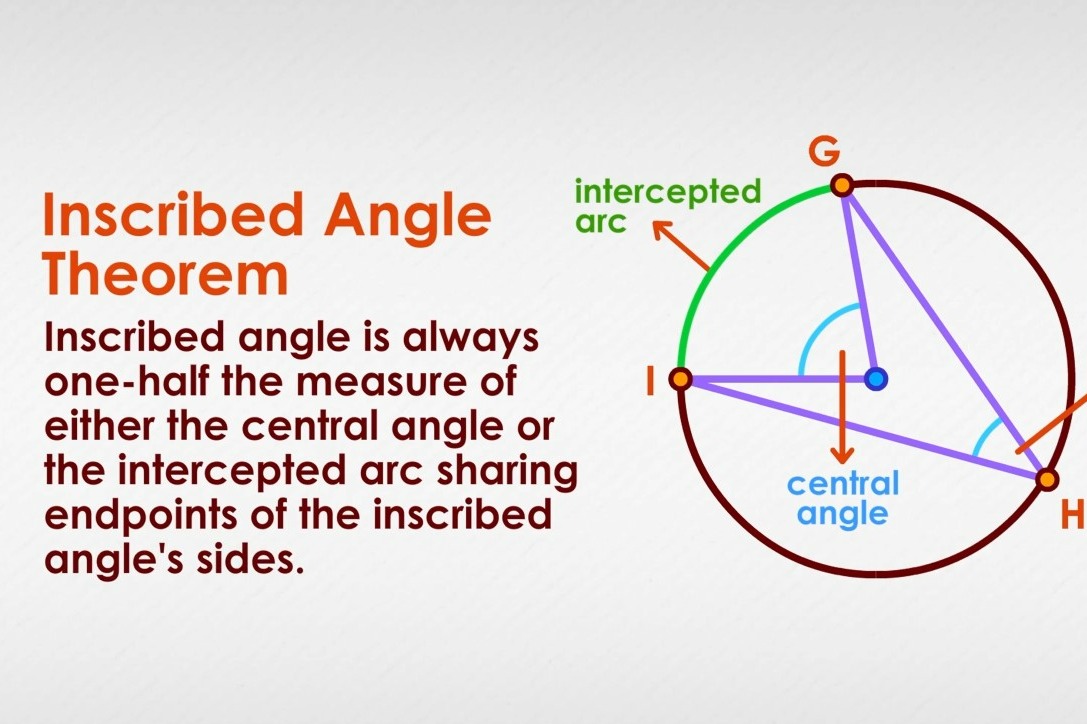
Note: The term "intercepted arc" refers to an arc "cut off" or "lying between" the sides of the specified angle. Central Angle A central angle is an angle formed by two radii with the vertex at the center of the circle. In a circle, or congruent circles, congruent central angles have congruent arcs. In a circle, or congruent circles, congruent central angles have congruent chords. Inscribed Angle An inscribed angle is an angle with its vertex "on" the circle, formed by two intersecting chords. An angle inscribed in a semicircle is a right angle. Called Thales Theorem.

The circular geometry is really vast. A circle consists of many parts and angles. These parts and angles are mutually supported by certain Theorems, e. Circles are all around us in our world. There exists an interesting relationship among the angles of a circle. Three types of angles are formed inside a circle when two chords meet at a common point known as a vertex. These angles are the central angle, intercepted arc, and the inscribed angle. An inscribed angle is an angle whose vertex lies on a circle, and its two sides are chords of the same circle. On the other hand, a central angle is an angle whose vertex lies at the center of a circle, and its two radii are the sides of the angle.

Formula of inscribed angle

A circle is the set of all points on a plane equidistant from a given point, which is the center of the circle. The only way to gather all the points that are the same distance from a point is to create a curved line. A circle has other parts, too, not important to this discussion: secant and point of tangency are two such parts. Circles are almost always indicated by the mathematical symbol followed by the circle's letter designation, its center point. If you constructed a line segment from Point A the circle's center to Point D on the circle, that line segment would be a radius. Running a chord from Point B to Point E would give you a diameter, which must run through the center of the circle. With circles, geometry becomes at once more interesting and more difficult. Combining curves and straight lines, circles create whole new possibilities.

La vie scolaire streaming vf

Angle Formed by Two Intersecting Chords. These cookies do not store any personal information. The inscribed angle is half the central angle which subtends the same arc. Everything you need to know on. Tools Tools. Further, it allows one to prove that when two chords intersect in a circle, the products of the lengths of their pieces are equal. A History of Greek Mathematics by Thomas Heath algebra timeline arithmetic timeline calculus timeline geometry timeline logic timeline mathematics timeline numbers prehistoric counting numeral systems list. In the above circle, O is the center point; angle A and angle D are inscribed angles that share the same arc BC. That means an intercepted arc can have dozens -- even hundreds -- even thousands! See how the inscribed angle theorem has simplified the calculation for you? Head to our arc length calculator! Find the length of an arc if the central angle is 2.

Home » Geometry » Angle » Inscribed Angle. An inscribed angle is an angle whose vertex lies on the circumference of a circle while its two sides are chords of the same circle.

NOTE: The re-posting of materials in part or whole from this site to the Internet is copyright violation and is not considered "fair use" for educators. Inscribed angle theorem - Inscribed angle formula The inscribed angle theorem establishes a relationship between the central and inscribed angles. It states that: The inscribed angle is equal to half of the central angle; and Changing the vertex of the inscribed angle does not change the angle so long as the vertex remains on the circle's circumference. A circle is unique because it does not have any corners or angles, which makes it different from other figures such as triangles , rectangles, and triangles. Luhn algorithm The Luhn algorithm calculator will help you test a number with Luhn validation and find one that successfully passes the test. Volume of a triangular prism Discover 6 ways to calculate the volume of a triangular prism with our easy-to-use calculator — meant for multiple types of prism faces! Middle School Math Tutors near me. In Elements Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Intersecting chords theorem Intersecting secants theorem Law of cosines Pons asinorum Pythagorean theorem Tangent-secant theorem Thales's theorem Theorem of the gnomon. Draw line OA. We also use third-party cookies that help us analyze and understand how you use this website. In a circle, inscribed angles that intercept the same arc are congruent. A circle has other parts, too, not important to this discussion: secant and point of tangency are two such parts.