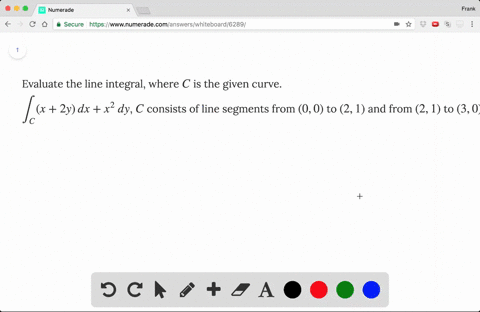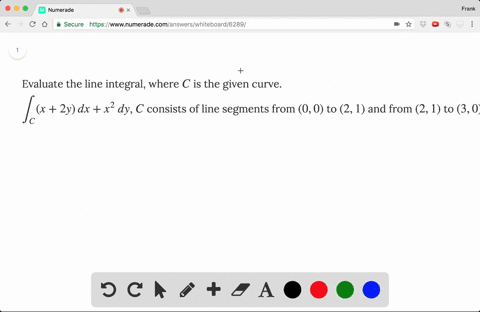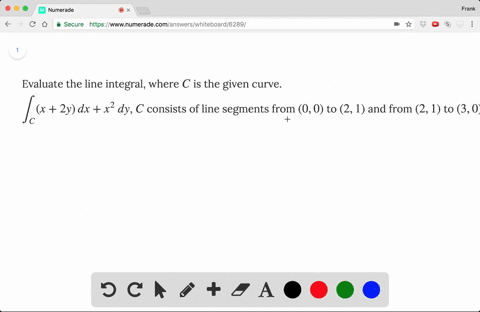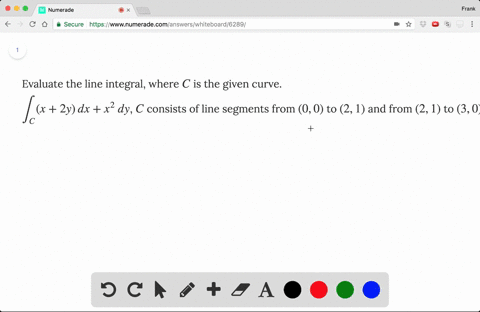
Evaluate the line integral where c is the given curve

In Calculus, a line integral is an integral in which the function to be integrated is evaluated along a curve.

Evaluate the line integral, where C is the given curve. Use a calculator or CAS to evaluate the line integral correct to four decimal places. Short Answer Step-by-step Solution. Now share some education! Short Answer Expert verified. Step by step solution Explanation of solution.

Evaluate the line integral where c is the given curve

Such an interval can be thought of as a curve in the xy -plane, since the interval defines a line segment with endpoints a , 0 a , 0 and b , 0 b , 0 —in other words, a line segment located on the x -axis. Suppose we want to integrate over any curve in the plane, not just over a line segment on the x -axis. Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see. A line integral gives us the ability to integrate multivariable functions and vector fields over arbitrary curves in a plane or in space. There are two types of line integrals: scalar line integrals and vector line integrals. Scalar line integrals are integrals of a scalar function over a curve in a plane or in space. Vector line integrals are integrals of a vector field over a curve in a plane or in space. A scalar line integral is defined just as a single-variable integral is defined, except that for a scalar line integral, the integrand is a function of more than one variable and the domain of integration is a curve in a plane or in space, as opposed to a curve on the x -axis. For a scalar line integral, we let C be a smooth curve in a plane or in space and let f f be a function with a domain that includes C. We chop the curve into small pieces. For each piece, we choose point P in that piece and evaluate f f at P. We can do this because all the points in the curve are in the domain of f.

Areas in polar coordinates 4. Calculus with Power Series

Q: Evaluate the line integral, where C is the given curve. Q: evaluate the line integral along the curve C. Q: Find the line integral of x ds over C where c is the line segment from 1,0 to 0,1 using two…. A: Given. A: Line integral.

Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see. A line integral gives us the ability to integrate multivariable functions and vector fields over arbitrary curves in a plane or in space. There are two types of line integrals: scalar line integrals and vector line integrals. Scalar line integrals are integrals of a scalar function over a curve in a plane or in space. Vector line integrals are integrals of a vector field over a curve in a plane or in space. We chop the curve into small pieces. The result is the scalar line integral of the function over the curve.

Evaluate the line integral where c is the given curve

To illustrate the idea, think about how it feels to run on a track on a windy day or to row a boat across a lake with a noticeable current? The path of the wind or the flow of the current might make it easier in one direction than the other, right? Interestingly, a line integral can help us map out where we benefited from the wind or the current and where those same forces hindered our progress. A line integral , called a curve integral or a path integral , is a generalized form of the basic integral we remember from calculus 1. But instead of being limited to an interval, [a,b], along the x-axis, we can explain more general curves along any path in the plane. Finally, we are ready to substitute everything into our line integral formula and integrate it over our interval. But the real superpower of line integrals is its ability to determine the work done by a force or work along a trajectory. Now, all we have to do is substitute everything into our line integral for vector fields formula and integrate.

Insulated bag uber

A: Note:-Our guidelines we are supposed to answer only one question. We want to compute each of the four integrals on the right-hand side using Equation 6. Because of Equation 6. Cross Multiplication Formula. Suppose that a piece of wire is modeled by curve C in space. Powers of sine and cosine 3. The second type of line integrals are vector line integrals, in which we integrate along a curve through a vector field. Maxima and minima 8. Short Answer Step-by-step Solution. Arc length can be thought of as the distance you would travel if you walked along the path of a curve. Q: Evaluate the integral a sin y ds where C is the line segment from 0, 3 to 4,6 ,. Green's Theorem 5.

In this section we are now going to introduce a new kind of integral. However, before we do that it is important to note that you will need to remember how to parameterize equations, or put another way, you will need to be able to write down a set of parametric equations for a given curve. You should have seen some of this in your Calculus II course.

We pick some points along the part of the parabola we're interested in, and connect adjacent points by straight lines; when the points are close together, the length of each line segment will be close to the length along the parabola. In Example 6. Square Root Of 3. You appear to be on a device with a "narrow" screen width i. This will be a much easier parameterization to use so we will use this. All we do is evaluate the line integral over each of the pieces and then add them up. Calculate the flux across C. For the following exercises, use a computer algebra system CAS to evaluate the line integrals over the indicated path. How would we compute the work done by F F in moving a particle along C? Q: evaluate the line integral along the curve C. Now that we can evaluate line integrals, we can use them to calculate arc length. Scalar line integrals are integrals of a scalar function over a curve in a plane or in space.