Cv2.solvepnpransac

PNP problem stands for Perspective N — points problem. It is a commonly known problem in computer vision. In this problem, cv2.solvepnpransac, we have to estimate the pose of a camera when the 2D projections of 3D points are given. In addition, we have to determine the distance between the camera and the cv2.solvepnpransac of points in the coordinate system, cv2.solvepnpransac.

Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community. Already on GitHub? Sign in to your account. It appears that the generated python bindings for solvePnPRansac in OpenCV3 have some type of bug that throws an assertion.

Cv2.solvepnpransac

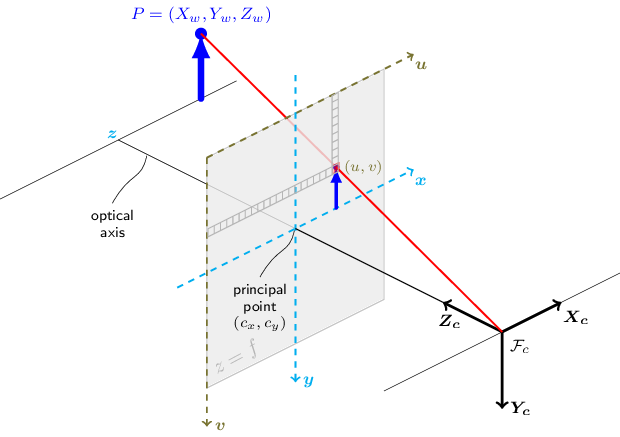
The functions in this section use a so-called pinhole camera model. You will find a brief introduction to projective geometry, homogeneous vectors and homogeneous transformations at the end of this section's introduction. For more succinct notation, we often drop the 'homogeneous' and say vector instead of homogeneous vector. The matrix of intrinsic parameters does not depend on the scene viewed. So, once estimated, it can be re-used as long as the focal length is fixed in case of a zoom lens. Combining the projective transformation and the homogeneous transformation, we obtain the projective transformation that maps 3D points in world coordinates into 2D points in the image plane and in normalized camera coordinates:. Real lenses usually have some distortion, mostly radial distortion, and slight tangential distortion. So, the above model is extended as:. Higher-order coefficients are not considered in OpenCV. Radial distortion is always monotonic for real lenses, and if the estimator produces a non-monotonic result, this should be considered a calibration failure. More generally, radial distortion must be monotonic and the distortion function must be bijective. A failed estimation result may look deceptively good near the image center but will work poorly in e. The optimization method used in OpenCV camera calibration does not include these constraints as the framework does not support the required integer programming and polynomial inequalities. See issue for additional information.

Would suggest changing the documentation re: the python bindings to reflect this, as this behavior is different than the 2, cv2.solvepnpransac. Vector of vectors of calibration pattern points in the cv2.solvepnpransac pattern coordinate space.

The function estimates an object pose given a set of object points, their corresponding image projections, as well as the camera matrix and the distortion coefficients. This function finds such a pose that minimizes reprojection error, that is, the sum of squared distances between the observed projections imagePoints and the projected using cv. The method used to estimate the camera pose using all the inliers is defined by the flags parameters unless it is equal to P3P or AP3P. In this case, the method EPnP will be used instead. Output rvec Output rotation vector see cv.

The functions in this section use a so-called pinhole camera model. You will find a brief introduction to projective geometry, homogeneous vectors and homogeneous transformations at the end of this section's introduction. For more succinct notation, we often drop the 'homogeneous' and say vector instead of homogeneous vector. The matrix of intrinsic parameters does not depend on the scene viewed. So, once estimated, it can be re-used as long as the focal length is fixed in case of a zoom lens.

Cv2.solvepnpransac

In this tutorial we will learn how to estimate the pose of a human head in a photo using OpenCV and Dlib. In many applications, we need to know how the head is tilted with respect to a camera. In a virtual reality application, for example, one can use the pose of the head to render the right view of the scene. For example, yawing your head left to right can signify a NO. But if you are from southern India, it can signify a YES! To understand the full repertoire of head pose based gestures used by my fellow Indians, please partake in the hilarious video below. Before proceeding with the tutorial, I want to point out that this post belongs to a series I have written on face processing. Some of the articles below are useful in understanding this post and others complement it.

Medal clasps and bars

Not set by default. The calculated fundamental matrix may be passed further to computeCorrespondEpilines that finds the epipolar lines corresponding to the specified points. It can be computed from the same set of point pairs using findFundamentalMat. This distortion can be modeled in the following way, see e. The distortion coefficients do not depend on the scene viewed. For every point in one of the two images of a stereo pair, the function finds the equation of the corresponding epipolar line in the other image. The functions in this section use a so-called pinhole camera model. F Output fundamental matrix. Output rvec Output rotation vector see cv. Otherwise R and T are initialized to the median value of the pattern views each dimension separately. Would suggest changing the documentation re: the python bindings to reflect this, as this behavior is different than the 2. These points were all generated in one of my test cases, and all the points are inliers.

PNP problem stands for Perspective N — points problem. It is a commonly known problem in computer vision. In this problem, we have to estimate the pose of a camera when the 2D projections of 3D points are given.

Parameter indicating whether the complete board was found or not. Parameters rotations Vector of rotation matrices. As you can see, the first three columns of P1 and P2 will effectively be the new "rectified" camera matrices. Reprojects a disparity image to 3D space. Output vector of distortion coefficients. In many common cases with inaccurate, unmeasured, roughly planar targets calibration plates , this method can dramatically improve the precision of the estimated camera parameters. The coordinates might be scaled based on three fixed points. The summary of the method: the decomposeHomographyMat function returns 2 unique solutions and their "opposites" for a total of 4 solutions. These points were all generated in one of my test cases, and all the points are inliers. Calculates an essential matrix from the corresponding points in two images from potentially two different cameras. In case of a projector-camera pair, newCameraMatrix is normally set to P1 or P2 computed by stereoRectify. Only 1 solution is returned. Parameters E The input essential matrix.