Common chord of two circles formula

Thus, this is precisely the common chord!

Hopefully I am thinking of the easiest way to solve the problem, but start by drawing the following diagram:. You can see the scalene triangle ABC in this diagram. Let's now redraw this without the circles:. You should recognize that the chord and the radial line AB are perpendicular, so a is the height of triangle ABC and d is its base. You can re-arrange each of the circle equations into standard circle form which allows you to read off the radius and the center position of each circle. Assign one radius as R and the other as r. Use the distance formula to calculate the distance between the two centers that's d.

Common chord of two circles formula

.

Cheers, Stephen La Rocque.

.

The chord of a circle can be stated as a line segment joining two points on the circumference of the circle. The diameter is the longest chord of the circle which passes through the center of the circle. The figure shown below represents the circle and its chord. In the circle above with center O, AB represents the diameter of the circle longest chord of a circle , OE represents the radius of a circle and CD represents the chord of a circle. Let us consider CD as the chord of a circle and points P and Q lying anywhere on the circumference of the circle. In this article, we will study what is a chord in a circle, chord length formulas, how to find the length of the chord, length of the common chord of two circles formulas, chord radius formulas, etc. There are two important formulas to find the length of the chords. The formula for the length of a chord is given as:.

Common chord of two circles formula

If we know the radii of two intersecting circles, and how far apart their centers are, we can calculate the length of the common chord. Circles O and Q intersect at points A and B. The radius of circle O is 16, and the radius of circle Q is 9.

Clown turkey in disguise

Let's now redraw this without the circles: You should recognize that the chord and the radial line AB are perpendicular, so a is the height of triangle ABC and d is its base. Practice worksheets in and after class for conceptual clarity. As well, any scalene triangle with known side lengths has an area that can be calculated using Heron's Formula. Kindergarten Worksheets. The length of the common chord can be easily evaluated using the Pythagoras theorem:. Sri Lanka. Maths Questions. Question from shubha, a student: please help me out with this problem. The angle of intersection of the two circles can be defined as the angle between the tangents to the two circles at their point s of intersection, which will be the same as the angle between the two radii at the point s of intersection. Hopefully I am thinking of the easiest way to solve the problem, but start by drawing the following diagram:. So calculate the area using Heron's formula and use that together with the distance d as the base to find the height a.

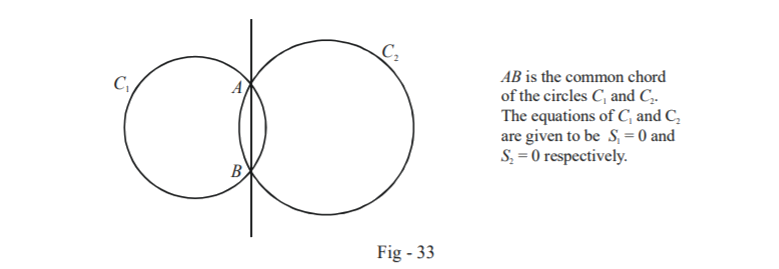
Now we need to find the equation of the common chord PQ of the given circles. Now subtracting the equation 4 from equation 3 we get,. Again, we observe from the above figure that the point Q x2, y2 lies on both the given equations.

Maths Questions. Let's now redraw this without the circles: You should recognize that the chord and the radial line AB are perpendicular, so a is the height of triangle ABC and d is its base. The angle of intersection of the two circles can be defined as the angle between the tangents to the two circles at their point s of intersection, which will be the same as the angle between the two radii at the point s of intersection. For a circle lying inside another circle, neither the radical axis nor the common chord exist:. As an exercise, verify that the following pairs of circles intersect orthogonally:. About Us. Now an interesting question arises. United States. The height of a triangle times half its base is the area of the triangle. It should be obvious that in case of intersecting or touching circles, the common chord or the common tangent is itself the radical axis. This line is termed the radical axis of the two circles. You can see the scalene triangle ABC in this diagram. For a situation as in Fig - 37 above, the radical axis exists but no common chord exists.