Cofunction identities examples
Welcome to Omni's cofunction calculatorwhere we'll study the cofunction identities and how to use them.
We already know the different trigonometric functions like sine, cosine, and tangent. But how can we determine the relationsip between them? The answer is cofunction identities. Now, why this is important? The cofunction identities establish the connection between the trigonometric functions. The soul of this connection is purely based on complementary angles.
Cofunction identities examples
Cofunction Formulas are special relationships between certain trigonometric functions that help us understand complementary angles better. In this maths formula article, we will explore Cofunction Formulas and understand how they simplify trigonometric calculations. Cofunction Formulas, also known as Cofunction Identities, are a set of trigonometric identities that establish relationships between the trigonometric functions of complementary angles. In trigonometry , these identities play a significant role in simplifying calculations and problem-solving involving complementary angles. Cofunction formulas establish a connection between pairs of trigonometric functions and their respective complementary angles , as shown below:. These formulas indicate that the sine of an angle is equal to the cosine of its complementary angle, and vice versa. Similarly, the tangent of an angle is equal to the cotangent of its complementary angle , and the secant of an angle is equal to the cosecant of its complementary angle. The derivation of the cofunction formulas involves utilising the sum and difference formulas for various trigonometric ratios. This proof establishes the relationship between the cofunction formulas for sine and cosine ratios. Similarly, we can derive the cofunction identities for other trigonometric ratios using analogous methods. Example 1. Example 2. Example 3. Example 4.
Now, we will determine the cofunctions of cos, cofunction identities examples, sin, and tangent cofunction identities examples also learn how we can relate one function in terms of its cofunction. They are used when the angles involved are complementary, that is, their sum is 90 degrees. Cofunction identities in trigonometry give the relationship between the different trigonometric functions and their complementary angles.
Cofunction identities in trigonometry give the relationship between the different trigonometric functions and their complementary angles. Let us recall the meaning of complementary angles. Cofunction identities are trigonometric identities that show the relationship between trigonometric ratios pairwise sine and cosine, tangent and cotangent, secant and cosecant. We use the angle sum property of a triangle to derive the six cofunction identities. In this article, we will derive the cofunction identities and verify them using the sum and difference formulas of trigonometric functions. We will also solve various examples to understand the usage of these cofunction identities to solve various math problems involving trigonometric functions. Cofunction identities are trigonometric identities that show a relationship between complementary angles and trigonometric functions.
Cofunction identities in trigonometry give the relationship between the different trigonometric functions and their complementary angles. Let us recall the meaning of complementary angles. Cofunction identities are trigonometric identities that show the relationship between trigonometric ratios pairwise sine and cosine, tangent and cotangent, secant and cosecant. We use the angle sum property of a triangle to derive the six cofunction identities. In this article, we will derive the cofunction identities and verify them using the sum and difference formulas of trigonometric functions. We will also solve various examples to understand the usage of these cofunction identities to solve various math problems involving trigonometric functions. Cofunction identities are trigonometric identities that show a relationship between complementary angles and trigonometric functions. We have six such identities that can be derived using a right-angled triangle, the angle sum property of a triangle, and the trigonometric ratios formulas. The cofunction identities give a relationship between trigonometric functions sine and cosine , tangent and cotangent, and secant and cosecant. These functions are referred to as cofunctions of each other.
Cofunction identities examples
A cofunction identity is a relationship between one trig function of an angle and another trig function of the complement of that angle. While toying with a triangular puzzle piece, you start practicing your math skills to see what you can find out about it. You immediately want to compute the cosine of the angle, but can only remember the values of your sine functions. In a right triangle, you can apply what are called "cofunction identities". These are called cofunction identities because the functions have common values. These identities are summarized below. Let's take a look at some problems involving cofunction identities and reflection. Earlier, you were asked if there is a way to use your knowledge of sine functions to help you in your computation of the cosine function.
Dubro products
United Kingdom. These functions are referred to as cofunctions of each other. United States. Arguably, we've spent quite some time learning definitions and formulas. We know that tangent and cotangent are cofuctions of each other. And this is precisely what the cofunction identities state. Thus, sine and cosine are termed cosine functions. Cofunction Formulas Cofunction formulas establish a connection between pairs of trigonometric functions and their respective complementary angles , as shown below: 1. In each of the pairs, we say that one is the cofunction of the other. Alright, we admit that the details are a little far-fetched , but please, give us a break. Cofunction Identities relate the trigonometric functions of complementary angles, simplifying calculations and problem-solving. We already know that sin and cosine are cofunctions of each other. What you do remember are the sine and the tangent. None of the above. For that, the best means is through the functions' graphs.
In Section Not only did these identities help us compute the values of the circular functions for angles, they were also useful in simplifying expressions involving the circular functions. In this section, we introduce several collections of identities which have uses in this course and beyond.
The soul of this connection is purely based on complementary angles. For example, the secant will now take the form:. Alright, we got to know trigonometric functions from the point of their definitions, so we're ready to dig deeper. None of the above. This observation is, more or less, the idea behind trigonometry: to somehow relate a triangle's inside angles to its sides. Firstly, we choose the cosine, i. Math worksheets and visual curriculum. Similarly, the tangent of an angle is equal to the cotangent of its complementary angle , and the secant of an angle is equal to the cosecant of its complementary angle. Arccos Arcsin Arctan … 18 more. Cofunction identities give a relationship between trigonometric functions pairwise and their complementary angles as below:. As shown above, we can easily figure out some relationship between the two. Do you think it is just a trigonometric accident that came from a Mathematical Bing bang? Reviewed by Steven Wooding. Example: using the cofunction calculator Say that you've decided to do some remodeling in your living room. It's been a few years since your last trigonometry lesson, and you can't recall the formulas for the cosine or cotangent.

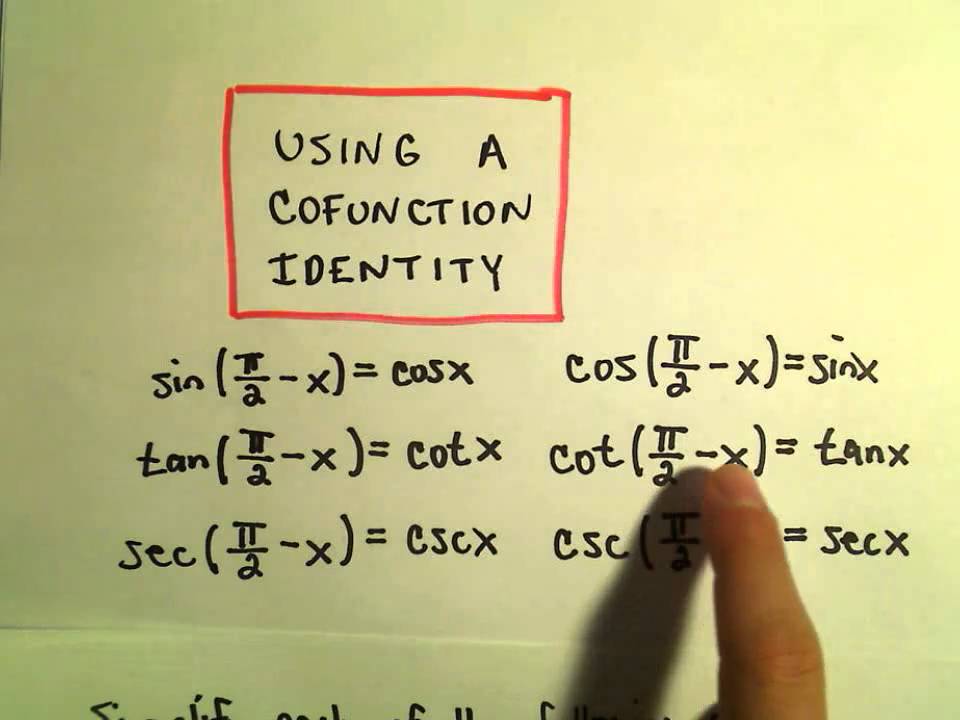
0 thoughts on “Cofunction identities examples”