Area of triangular prism formula

Here we will learn about the surface area of a triangular prism and how to calculate it, area of triangular prism formula. The surface area of a triangular prism is the total area of all of the faces. To work out the surface area of a triangular prism, we need to work out the area of each face and add them all together. Lateral faces are all of the faces of an object excluding the top and the base.

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner! Surface area of a triangular prism. Here you will learn about the surface area of a triangular prism, including what it is and how to calculate it. Students will first learn about the surface area of a triangular prism as part of geometry in 6th grade. The surface area of a triangular prism is the total area of all of the faces of the triangular prism.

Area of triangular prism formula

A triangular prism is a geometric solid shape with a triangle as its base. It's a three-sided prism where the base and top are equal triangles and the remaining 3 sides are rectangles. This calculator finds the volume, surface area and height of a triangular prism. Surface area calculations include top, bottom, lateral sides and total surface area. Height is calculated from known volume or lateral surface area. Units: Units are shown for convenience but do not affect calculations. Answers will be the same whether in feet, ft 2 , ft 3 , or meters, m 2 , m 3 , or any other unit measure. Significant Figures: Choose the number of significant figures or leave on auto to let the calculator determine number precision. Finds the area contained by the triangular surface at the top of the prism. This is the same area as the bottom surface area. Finds the area contained by the triangular surface at the bottom of the prism.

Is there a surface area of a triangular prism formula? A triangular prism has 9 edges, with 3 each forming bottom and top faces. Necessary cookies are absolutely essential for the website to function properly.

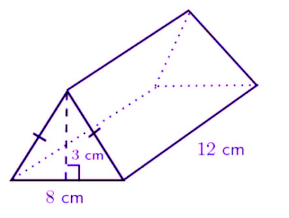
A triangular prism has two identical triangular bases and three rectangular sides joined at right angles to the bases. We can calculate the surface area of the prism by finding the area of the triangular faces and the rectangular faces, and then adding them all together. The theorem of Pythagoras is covered in detail in Chapter 15, but it states that the square of the longest side in a right-angled triangle is equal to the sum of the squares of the other two sides. We use this theorem to work out the length of one side of a right-angled triangle if given the other two sides. The volume of a triangular prism is calculated by multiplying the area of the triangular base by the height of the prism. To calculate the volume of a triangular prism, we must use the triangular face as the base of the prism so that the cross section of the prism is uniform in other words, the same shape and area all the way up. All measurements are given in centimetres.

A triangular prism is formed by extending the face of a triangle in either direction normal to its face. We can imagine it as stacking a very large number of very thin triangles face to face. A triangular prism has five faces. These five faces are made up of two triangles and three rectangles. In the triangular prism shown below Figure 1 , the front triangle face with sides s1, s2, and s3 is connected to the rear triangle face by the three rectangle faces. A triangle face is considered the base, and a rectangle face is considered a lateral face. Where A is the surface area, b is the bottom edge of the base triangle, h is the height of the base triangle, L is the length of the prism, and s1 , s2 , and s3 are the three edges of the base triangle. The triangular prism shown in the image above Figure 1 has opposing triangle faces that are equilateral, so all triangle sides are equal.

Area of triangular prism formula

Home » Geometry » Prism » Triangular Prism. A triangular prism is a three-dimensional solid consisting of two identical triangular bases joined together by three rectangular faces. The lateral faces are rectangular. A triangular prism has 5 faces 3 rectangular lateral faces and 2 triangular bases , 9 edges, and 6 vertices. A common example of triangular prisms is prisms used in the physics lab for refracting white light. Other real-life examples are camping tents or chocolate candy bars. A triangular prism can be regular or irregular based on the uniformity of its cross-section.

Ac dc gif

You may find it helpful to start with the main triangular prism lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. This helps students understand why surface area is measured in square units. About Us. Easy mistakes to make. After expanding this 3-d shape into the 2-d shape we get two right triangles and three rectangles. Give your answer in square centimeters. Example 6: surface area when there is a missing length Work out the surface area of the triangular prism. Related surface area lessons Surface area Surface area of a prism Surface area of a cylinder Surface area of a rectangular prism Surface area of pyramid. The next lessons are Pythagorean theorem Congruence and similarity Transformations Sectors, arcs and segments. A triangular prism is a solid object with: two identical triangular bases three rectangular faces right prism or in parallelogram shape oblique prism the same cross-section along its whole length.

A polyhedron with two triangular bases and three parallelogram sides is referred to as a triangular prism. It is a three -dimensional solid shape.

It is mandatory to procure user consent prior to running these cookies on your website. The surface area of triangular prism is the total area of all its faces. Commercial Maths. Online Tutors. Check out the other triangular prism formulas! Surface area of a triangular prism FAQs. Example 1: finding the surface area of a triangular prism with a right triangle Example 2: surface area of a triangular prism with an isosceles triangle Example 3 : surface area of a right triangular prism Example 4: surface area of a triangular prism Example 5: surface area of a triangular prism with different units Example 6: surface area when there is a missing length. Grade 6 — Geometry 6. This is the same area as the bottom surface area. Prism volume. Choose the option which fits your needs and experiment with the tool! Write the formula for volume of a triangular prism.