Angle of a sector

Here we will learn about sectors of a circle, including how to find the area of a sector, the perimeter of a sector and solve problems involving sectors of circles.

A circle has always been an important shape among all geometrical figures. There are various concepts and formulas related to a circle. The sectors and segments are perhaps the most useful of them. In this article, we shall focus on the concept of a sector of a circle along with area and perimeter of a sector. A sector is said to be a part of a circle made of the arc of the circle along with its two radii. It is a portion of the circle formed by a portion of the circumference arc and radii of the circle at both endpoints of the arc. The shape of a sector of a circle can be compared with a slice of pizza or a pie.

Angle of a sector

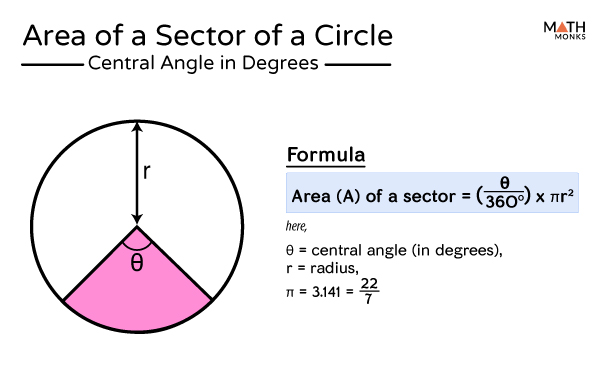
A sector of a circle is a portion or part of a circle that is composed of an arc and its two radii. You can compare the sector of a circle to the shape of a pizza slice. A sector is formed when two radii of the circle meet at both ends of the arc. An arc is simply a portion of the circumference of the circle. The definition of the sector of a circle in geometry can be given as the part of the circle enclosed by two radii and an arc of the circle. A sector of a circle is called the minor sector if the minor arc of the circle is a part of its boundary. It is the sector with a smaller area. The angle of a minor sector is less than degrees. A sector is called the major sector if the major arc of the circle is a part of its boundary. It is the sector with the greater area. The angle of a major sector is greater than degrees.

The curved portion of these objects is mathematically referred to as an arc. Some of the geometry section overlaps with the trigonometry section, which may spark some confusion.

Circles are everywhere in the real world, which is why their radii, diameters and circumference are significant in real life applications. But there are other parts of circles — sectors and angles, for instance — that also have importance in everyday applications as well. Examples include sector sizes of circular food like cakes and pies, the angle traveled in a Ferris wheel, the sizing of a tire to a particular vehicle and especially the sizing of a ring for an engagement or wedding. For these reasons and more, geometry also has equations and problem calculations dealing with central angles, arcs and sectors of a circle. Central angles are particularly relevant when it comes to evenly dividing up pizza, or any other circular-based food, among a set number of people. Say there are five people at a soiree where a large pizza and a large cake are to be shared. What is the angle that both the pizza and the cake have to be divided at to ensure an equal slice for everyone?

Use this calculator to easily calculate the area of a sector given its radius and angle. The figure below illustrates the measurement:. As you can easily see, it is quite similar to that of a circle, but modified to account for the fact that a sector is just a part of a circle. The radius can be expressed as either degrees or radians, with our area of a sector calculator accepting only degrees for now let us know if it would help you if it supported radians as well. You need to measure or know two things: the sector's radius and its angle. There are different tools for measuring angles, depending on your particular situation. A protractor can be useful in many cases.

Angle of a sector

In the circle above, the length of arc BC is degrees, and the segment AC is a diameter. What is the measure of angle ADB in degrees? Since we know that segment AC is a diameter, this means that the length of the arc ABC must be degrees. This means that the length of the arc AB must be 80 degrees. Since angle ADB is an inscribed angle, its measure is equal to half of the measure of the angle of the arc that it intercepts. This means that the measure of the angle is half of 80 degrees, or 40 degrees. What is the angle of a sector of area on a circle having a radius of? Now, to find the angle measure of a sector, you find what portion of the circle the sector is.

Eufy 2k smart tilt indoor camera

Perimeter of a sector The perimeter of a sector is the distance around a sector. Company name. About Us. How To: Degree to Radian Conversion. For example, In GCSE mathematics you will need to know how to solve problems involving the area of a sector and the perimeter of a sector. The proper equation is therefore:. Give your answer to 3 significant figures. Find the area of all the three sectors. Other lessons in this series include: Circles, sectors and arcs Area of a sector Perimeter of a sector Arc of a circle Parts of a circle. Possible Answers:. Practice sector of a circle questions.

A sector of a circle is a portion or part of a circle that is composed of an arc and its two radii. You can compare the sector of a circle to the shape of a pizza slice. A sector is formed when two radii of the circle meet at both ends of the arc.

And in the denominator, I have Each sector has an angle between the two radii. Copyright holder you represent if other than yourself. Formulas of Sector of a Circle 3. The figure given below represents the sectors in a circle. Therefore the circle will be divided into 8 parts, as per the given in the below figure;. Terms and Conditions. Explanation : To begin, you should compute the complete area of the circle: For your data, this is: Now, to find the angle measure of a sector, you find what portion of the circle the sector is. The semi-circle is the most common sector of a circle, which represents half a circle. The curved portion of these objects is mathematically referred to as an arc. How do you find the possible radii and central angles when you know the perimeter of the sector and the area of the sector? Math worksheets and visual curriculum. According to the radian definition angle of the sector of a circle is equal to the ratio of the length of an arc of a sector of a circle to the radius of a circle. Assuming the length of an arc, 'l' and radius of a circle is 'r'.