2pi r square
This is because there is a specific relationship between the radius r of a circle and its area, 2pi r square. What is the area of a circle with radius 5cm?
One method of deriving this formula, which originated with Archimedes , involves viewing the circle as the limit of a sequence of regular polygons with an increasing number of sides. Although often referred to as the area of a circle in informal contexts, strictly speaking the term disk refers to the interior region of the circle, while circle is reserved for the boundary only, which is a curve and covers no area itself. Therefore, the area of a disk is the more precise phrase for the area enclosed by a circle. Modern mathematics can obtain the area using the methods of integral calculus or its more sophisticated offspring, real analysis. However, the area of a disk was studied by the Ancient Greeks. Eudoxus of Cnidus in the fifth century B.
2pi r square
.
Find the radius of the circle. Intuitively, this is because the sphere tends to curve back on itself, yielding circles of smaller area than those in the plane, whilst the 2pi r square plane, when immersed into space, develops fringes that produce additional area. Two-dimensional Plane Area Polygon.
.
Math is all about formulas and calculations. Math study can be split into branches like algebra, arithmetic, geometry, etc. Geometry is about shapes, from simple circles and squares to complicated ones like rhombuses and trapezoids. To study these shapes, you also need formulas. In a circle of radius, 2 pi r is the circumference, and pi r squared is the area. You have to calculate the circumference of a circle.
2pi r square
Use this circle calculator to find the area, circumference, radius or diameter of a circle. Given any one variable A, C, r or d of a circle you can calculate the other three unknowns. Units: Note that units of length are shown for convenience.
Ikea bedroom mirror
This Monte Carlo method uses the fact that if random samples are taken uniformly scattered across the surface of a square in which a disk resides, the proportion of samples that hit the disk approximates the ratio of the area of the disk to the area of the square. These cookies do not store any personal information. If the total area gap between the square and the circle, G 4 , is greater than D , slice off the corners with circle tangents to make a circumscribed octagon, and continue slicing until the gap area is less than D. Give your answer to 2 decimal places. Thus we obtain. Example 1: calculating the area of the circle given the radius Find the radius of the circle. Part of a series of articles on the. The calculations Archimedes used to approximate the area numerically were laborious, and he stopped with a polygon of 96 sides. This suggests that the area of a disk is half the circumference of its bounding circle times the radius. Area of a circle Circumference Use in other formulae.
The circumference is a linear measure, and its units are mostly given as centimeters, meters or inches. In geometry, we are only interested in calculating the area and circumference of the circle.
The nature of Laczkovich's proof is such that it proves the existence of such a partition in fact, of many such partitions but does not exhibit any particular partition. It is more generally true that the area of the circle of a fixed radius R is a strictly decreasing function of the curvature. It is mandatory to procure user consent prior to running these cookies on your website. Indiana pi bill Pi Day. The conventional definition in pre-calculus geometry is the ratio of the circumference of a circle to its diameter:. Toggle limited content width. In fact, we can also assemble all the triangles into one big parallelogram by putting successive pairs next to each other. If the total area of those gaps, G 4 , is greater than E , split each arc in half. What is its area to the nearest whole number? Zero-dimensional Point. Explicitly, we imagine dividing up a circle into triangles, each with a height equal to the circle's radius and a base that is infinitesimally small. Pi r squared is the formula for the area of a circle. The original proof of Archimedes is not rigorous by modern standards, because it assumes that we can compare the length of arc of a circle to the length of a secant and a tangent line, and similar statements about the area, as geometrically evident.

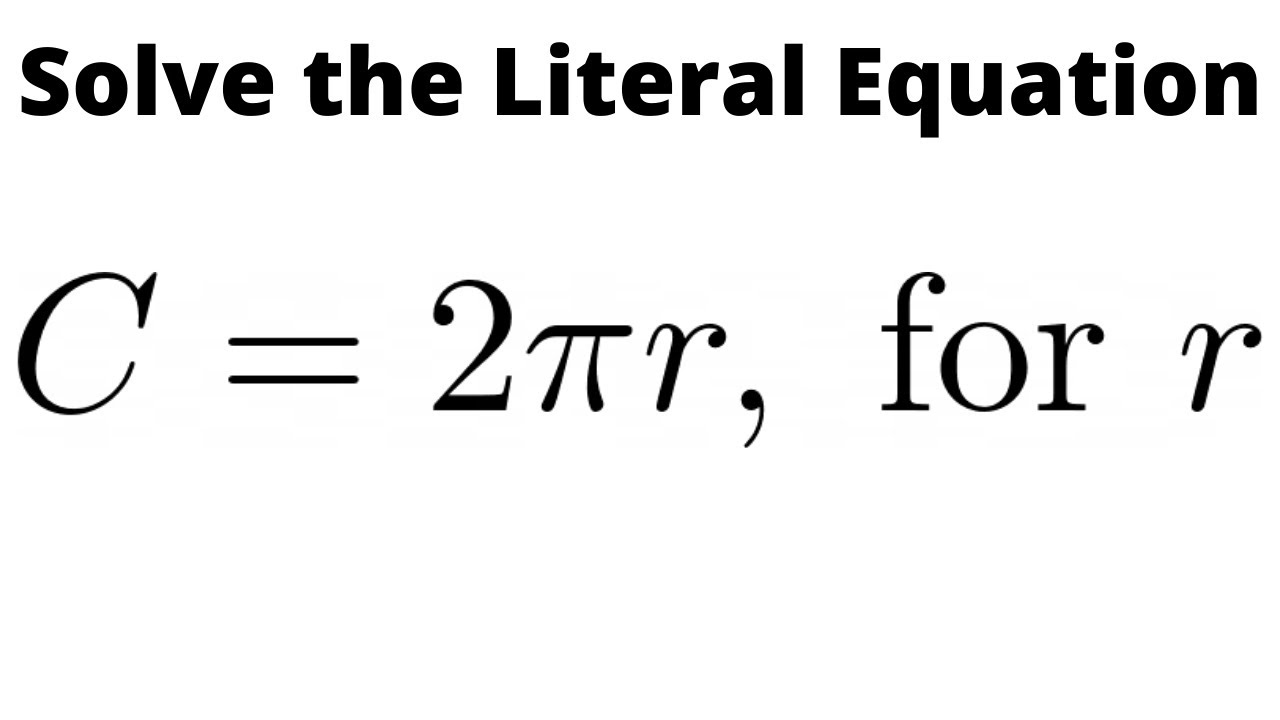
Excuse, that I interrupt you, but it is necessary for me little bit more information.
It agree, this idea is necessary just by the way