2011 calculus bc free response
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. AP Calculus BC About About this video Transcript. Volume of a solid of rotation and Chain Rule for rates of change. Created by Sal Khan.
2011 calculus bc free response
.
So once again, f of x is going to be approximately equal to.
.
If you're seeing this message, it means we're having trouble loading external resources on our website. AP Calculus BC Arc length for a curve. So let's draw some axes here to just make sure and you wouldn't obviously have to do this if you were doing it under time pressure during the actual AP exam but my point here to make sure we all are understanding what's going on. Well they tell us; x 0 is 0 so x is 0 and y 0 is -4 so we're at the point 0, I'll just say that's 21 right over there. So this is 21 and we figured this out in the last problem, I think it was And between these point who knows what the path is.
2011 calculus bc free response
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. AP Calculus BC About About this video Transcript. Position and slope of particle's path at a given time. Created by Sal Khan. Want to join the conversation? Log in. Sort by: Top Voted.
Typer racer
Now part c. So once again, f of x is going to be approximately equal to. This is what we figured out in part A. We can rewrite this as pi over 4 times 4e to the 4x. The region R is rotated about the x-axis to form a solid. AP Calculus BC And since we're assuming this is a Taylor series, the first term is going to be the lowest degree, then we're going to keep going at higher degree terms. Those are the first four non-zero terms of cosine of x. Aaron Williams. Pi times-- e to the 2x squared is e to the 4x, just 2x times 2.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos.
And we have this negative sign out here. Well, the radius is the height between the x-axis and the function. We have this term-- let me pick a nice color here-- we have this term, because we have a 1 coefficient. Use those-- that was found in part A-- to write the first four non-zero terms of the Taylor series for f about x equals 0. I dont think so. Right, because this right over here, this is x is equal to k, this is x is equal to 0, we take the sum of all the disks. So we want to take an infinite sum of these infinitely thin disks. And then, we don't have any first degree terms. So this would be the volume of this little disk over here that has a very small infinitesimally wide depth. And so if we say that h of x is equal to cosine of x, then h of 0, is going to be equal to cosine of 0, which is equal to 1. So it's going to be minus x to the 6th over 3 factorial plus x to the 6th over 6 factorial. So the derivative of V with respect to k is equal to pi over 4 times the derivative in here. We are going to evaluate it from 0 to k. It's a little bit of a cross section of this solid.

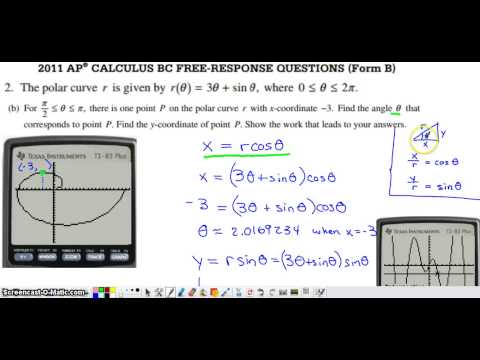
I risk to seem the layman, but nevertheless I will ask, whence it and who in general has written?