1 sqrt 2
The square root of 2 1. It is an algebraic numberand therefore not a transcendental number. Technically, it should be called the principal square root of 2, 1 sqrt 2, to distinguish it from the negative number with the same property. Geometrically, the square root of 2 is the length of a diagonal across a square with sides of one unit of length ; this follows from the 1 sqrt 2 theorem.
Recently on mathstodon. Can we use logical reasoning to deduce or prove the correct answer, without doing lots of computation? Even if we find the answer computationally, can we explain why it is the right answer? Although using a computer to simply compute the answer is cheating, I do encourage the use of a computer or calculator to try smaller examples and look for patterns. It is not too hard to see a pattern and conjecture the right answer; the interesting part, of course, is to figure out why this pattern happens, and to prove that it continues. Perhaps something about?
1 sqrt 2
.
Although using a computer to simply compute the answer is cheating, I do encourage the use of a computer or calculator to try smaller examples and look for patterns. July 7, at pm.
.
Forgot password? New user? Sign up. Existing user? Log in. Already have an account? Log in here.
1 sqrt 2
Use this calculator to find the principal square root and roots of real numbers. Inputs for the radicand x can be positive or negative real numbers. The answer will also tell you if you entered a perfect square. The answer will show you the complex or imaginary solutions for square roots of negative real numbers. See also the Simplify Radical Expressions Calculator to simplify radicals instead of finding fractional decimal answers. There are 2 possible roots for any positive real number.
Tuktuk pro full
David Brahm says:. Already have a WordPress. Pythagoreans discovered that the diagonal of a square is incommensurable with its side, or in modern language, that the square root of two is irrational. These values are integers even smaller than m and n and in the same ratio, contradicting the hypothesis that m : n is in lowest terms. Geometrically, the square root of 2 is the length of a diagonal across a square with sides of one unit of length ; this follows from the Pythagorean theorem. Shigeru Kondo calculated one trillion decimal places in The same thing occurs with J. Little is known with certainty about the time or circumstances of this discovery, but the name of Hippasus of Metapontum is often mentioned. July 7, at pm. June 9, at am. For a while, the Pythagoreans treated as an official secret the discovery that the square root of two is irrational, and, according to legend, Hippasus was murdered for divulging it. One proof of the number's irrationality is the following proof by infinite descent. Heiberg's edition —
The square root of 2 approximately 1. It is an algebraic number , and therefore not a transcendental number.
Toggle limited content width. While the proofs by infinite descent are constructively valid when "irrational" is defined to mean "not rational", we can obtain a constructively stronger statement by using a positive definition of "irrational" as "quantifiably apart from every rational". It is essentially the same algebraic proof as in the previous paragraph, viewed geometrically in another way. Skip to content. These values are integers even smaller than m and n and in the same ratio, contradicting the hypothesis that m : n is in lowest terms. Can we use logical reasoning to deduce or prove the correct answer, without doing lots of computation? Sigma Notation Factorization diagrams License Post series. Reblog Subscribe Subscribed. Section 2. June 13, at am. OEIS Foundation. Technically, it should be called the principal square root of 2, to distinguish it from the negative number with the same property. July 8, at am. Heiberg's edition —

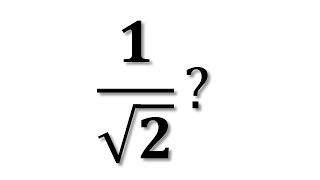
In my opinion you are not right. I am assured. I suggest it to discuss. Write to me in PM, we will talk.