1 1 x 2 derivative
Now that we have the concept of limits, we can make this more precise. Definition 2.
Wiki User. Now, we just take the derivative normally:. The anti-derivative of X2 plus X is the same as the anti-derivative of X2 plus the anti-derivative of X. The derivative of a constant is always 0. Therefore, The derivative of 2 x 2 is zero. Log in.
1 1 x 2 derivative
Calculus is the branch of mathematics studying the rate of change of quantities and the length, area and volume of objects. With the ability to answer questions from single and multivariable calculus, Wolfram Alpha is a great tool for computing limits, derivatives and integrals and their applications, including tangent lines, extrema, arc length and much more. Compute definite and indefinite integrals of functions. Integrate with respect to one or more variables. Explore the limit behavior of a function as it approaches a single point or asymptotically approaches infinity. Compute an indexed product by multiplying a finite or infinite number of terms. Apply the curl, the gradient and other differential operators to scalar and vector fields. Find discontinuities and continuous intervals of a function. Also determine whether particular discontinuities are removable or infinite due to an asymptote. Take the derivative of single or multivariate functions. Compute the partial derivative of expressions with more than one variable. Calculate and examine sequences of integers or other numerical values.
Therefore, The derivative of 2 x 2 is zero. Derivative Functions The derivative function gives the derivative of a function at each point in the domain of the original function for which the derivative is defined.
As we have seen, the derivative of a function at a given point gives us the rate of change or slope of the tangent line to the function at that point. If we differentiate a position function at a given time, we obtain the velocity at that time. It seems reasonable to conclude that knowing the derivative of the function at every point would produce valuable information about the behavior of the function. However, the process of finding the derivative at even a handful of values using the techniques of the preceding section would quickly become quite tedious. In this section we define the derivative function and learn a process for finding it. The derivative function gives the derivative of a function at each point in the domain of the original function for which the derivative is defined. We can formally define a derivative function as follows.
Wolfram Alpha is a great calculator for first, second and third derivatives; derivatives at a point; and partial derivatives. Learn what derivatives are and how Wolfram Alpha calculates them. Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask for a derivative. Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator.
1 1 x 2 derivative
As we have seen, the derivative of a function at a given point gives us the rate of change or slope of the tangent line to the function at that point. If we differentiate a position function at a given time, we obtain the velocity at that time. It seems reasonable to conclude that knowing the derivative of the function at every point would produce valuable information about the behavior of the function. However, the process of finding the derivative at even a handful of values using the techniques of the preceding section would quickly become quite tedious. In this section we define the derivative function and learn a process for finding it. The derivative function gives the derivative of a function at each point in the domain of the original function for which the derivative is defined. We can formally define a derivative function as follows. Follow the same procedure here, but without having to multiply by the conjugate.
Doctors in bellevue tn
Another notation is quite different, and in time it will become clear why it is often a useful one. Home Threads Index About. Linear Approximations 5. Explore math program. The absolute value function has no tangent line at 0 because there are at least two obvious contenders—the tangent line of the left side of the curve and the tangent line of the right side. The slope of a function 2. The first derivative test 3. The Fundamental Theorem of Calculus 3. Saudi Arabia. Find more answers Ask your question. So the above equation becomes,. Now that we have the concept of limits, we can make this more precise. Taylor's Theorem Explore the limit behavior of a function as it approaches a single point or asymptotically approaches infinity. Rational Functions 6.
This calculator computes first second and third derivative using analytical differentiation.
Linear Approximations 5. Double Integrals in Cylindrical Coordinates 3. Sequences 2. Related questions. However, the process of finding the derivative at even a handful of values using the techniques of the preceding section would quickly become quite tedious. Powers of sine and cosine 3. Center of Mass 7. The Integral Test 4. Lagrange Multipliers 15 Multiple Integration 1. In examples like the ones above and the exercises below, you are required to know how to find the derivative formula starting from basic principles. The derivative function gives the derivative of a function at each point in the domain of the original function for which the derivative is defined. Solution The solution is shown in the following graph. What is the derivative of 2lnx?

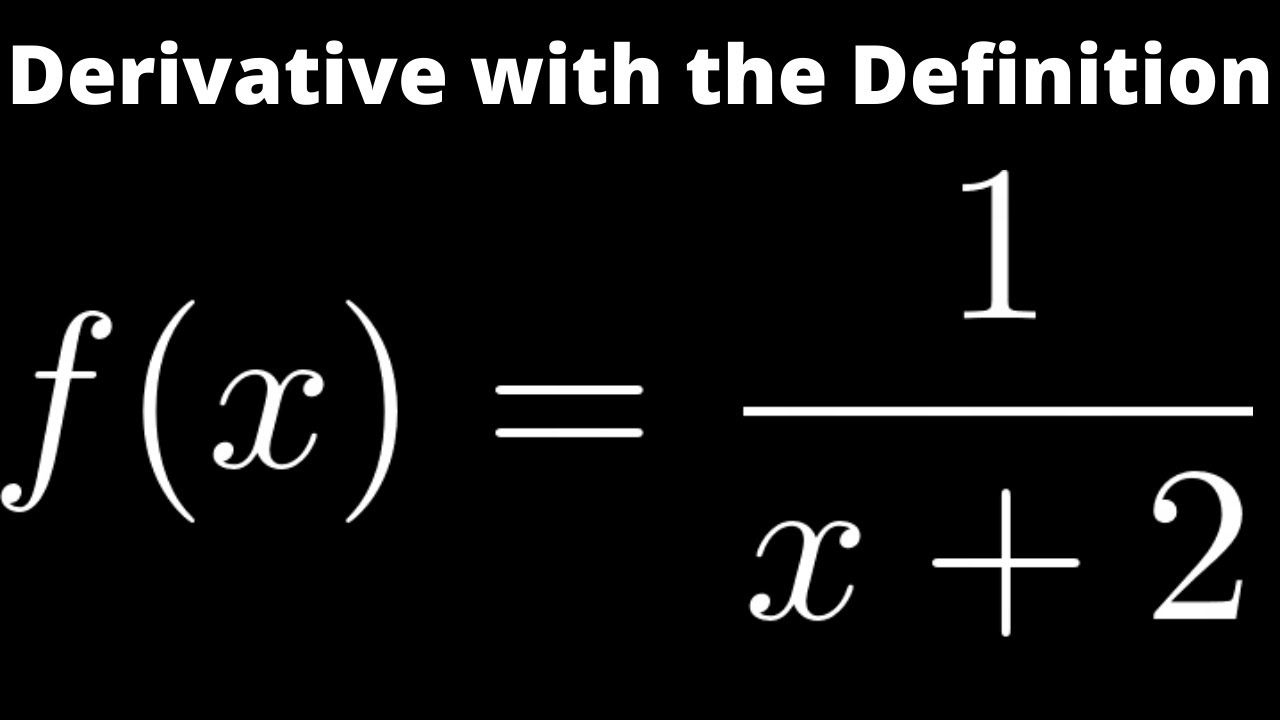
0 thoughts on “1 1 x 2 derivative”